Unité Centrale de Traitement : Processeur (CPU) - Architecture et Fonctionnement
Unité Centrale de Traitement : Processeur (CPU)
1 - Introduction
L'unité centrale de traitement (CPU : Central Processing Unit), encore dénommée processeur ou microprocesseur, est l'élément de l'ordinateur qui interprète et exécute les instructions d'un programme. C'est le cerveau de l'ordinateur. Mais on trouve aussi des processeurs, dits spécialisés, qui peuvent décharger l'unité centrale et assurer des tâches en parallèle. Ceci est très fréquent pour la gestion des entrées/sorties.
Un processeur est aujourd'hui un circuit électronique à très haute densité d'intégration (ULSI : Ultra Large Scale Integration), qui peut compter quelques dizaines de millions de transistors. Le premier circuit de ce type a été créé par Intel en 1971 : le 4004 conçu pour équiper des calculatrices. Il comptait alors 2300 transistors pour 46 instructions. La loi de Moore, formulée en 1965 par un des fondateurs de la compagnie Intel, qui prédit un doublement des capacités des processeurs tous les 18-24 mois, a jusqu'à présent été relativement bien suivie. Il ne s'agit pas seulement de l'augmentation de la fréquence de fonctionnement ou du nombre de transistors. Les concepteurs cherchent aussi à augmenter la quantité de traitement par cycle d'horloge.
Une unité centrale se compose d'au moins deux unités fonctionnelles : l'unité de commande et l'unité de calcul. A l'origine celle-ci s'identifiait à l'unité arithmétique et logique, chargée de l'exécution des opérations booléennes et des opérations arithmétiques (addition, soustraction, multiplication, division, comparaison, etc.) pour des entiers. En parallèle à cette unité, on peut trouver une unité de calcul sur les réels ainsi qu'une unité de traitement dédiée aux opérations multimédia (traitement des images et du son).
A côté de ces deux unités fonctionnelles on trouve une interface de gestion des communications sur le bus externe, ainsi qu'une mémoire cache. Celle-ci est baptisée de premier niveau car située à proximité immédiate du cœur du processeur. Mais depuis quelques années, les concepteurs ont été amenés à embarquer également la mémoire de second niveau. Ces caches peuvent être scindés pour séparer les instructions et les données (architecture Harward).
L'unité de commande contient une unité chargée du décodage des instructions, une unité pour le calcul des adresses des données à traiter. On y trouve également le séquenceur qui contrôle le fonctionnement des circuits de l'unité de calcul nécessaires à l'exécution de chaque instruction.
L'unité centrale comprend un certain nombre de registres pour stocker des données à traiter, des résultats intermédiaires ou des informations de commande. Parmi ces registres certains servent pour les opérations arithmétiques ou logiques, d'autres ont des fonctions particulières comme le registre instruction (RI) qui contient l'instruction à exécuter, le compteur ordinal (CO) qui pointe sur la prochaine instruction ou un registre d'état (RE ou PSW : Processor Status Word) contenant des informations sur l'état du système (retenue, dépassement, etc.).
La figure 1 présente un schéma général très simplifié de l'organisation de l'unité centrale, sans tenir compte de la présence d'une mémoire cache et de l'interface avec le bus externe.
Avant d'étudier le fonctionnement de l'unité de commande nous allons passer rapidement au travers de certains éléments de l'ALU, c'est-à-dire le traitement numérique et logique des entiers. Nous avons, en fait, déjà étudié dans les chapitres précédents les principales fonctions intervenant dans l'ALU pour des entiers non signés : comparaison, addition, soustraction, décalage, etc. Nous allons étendre cette étude aux entiers signés et pour cela nous commençons par étudier la représentation des nombres en machine.
2 - Représentation des nombres
a) Entiers non signés
Les entiers positifs ou nuls peuvent être codés en binaire pur. A l'aide de n bits nous pouvons représenter 2n nombres compris entre 0 et 2n – 1 :
Sur le papier on utilise souvent les notations, plus compactes, octale ou hexadécimale : un chiffre (de 0 à 8) en octal représente 3 bits et un caractère (de 0 à F) hexadécimal permet de représenter 4 bits (table 1). Ainsi un octet s'écrit comme deux caractères hexadécimaux.
Si on n'utilise qu'une seule représentation binaire des entiers non signés, on rencontre plusieurs manières de coder les entiers signés. Nous allons en étudier quelques-unes. La table 2 présente une illustration sur 9 bits de ces différents codes : le bit de signe, le plus à gauche, y est mis en évidence.
b) Entiers signés sous la forme signe et valeur absolue
L'idée la plus naturelle pour coder des entiers signés consiste à ajouter le signe sous la forme d'un bit supplémentaire : 0 pour les entiers positifs et 1 pour les entiers négatifs. Soit pour n+1 bits :
On code alors
c) Entiers signés en complément vrai
Nous avons vu que la représentation en complément à deux facilite les opérations arithmétiques d'addition et de soustraction. Notons A+ le complément vrai, ou complément à deux, d'un entier positif, défini par :
Il est facile de vérifier que :
donc :
Par exemple :
Le complément vrai d'un entier peut donc être assimilé à son opposé. Considérons le codage sur n+1 bits. Par convention nous choisissons d'écrire tout entier positif avec le bit de plus haut poids an à 0 et sa valeur algébrique sur n bits. Nous pouvons ainsi coder 2n entiers positifs de 0 à 2n − 1. Prenons le complément vrai de tous ces mots de n+1 bits. Commençons par le zéro. Son complément est constitué de (n+1) bits à 1. En additionnant 1, pour passer au complément vrai, la retenue se propage jusqu'au dernier bit et nous obtenons (n+1) bits à 0 :
Dans cette représentation, il n'y a donc qu'un seul zéro. Tout autre entier positif possède au moins un bit à 1. Dans le complément tous les bits à 1 deviennent des 0. Lors de l'addition de 1, pour passer au complément vrai, le premier bit à 0 arrête la propagation de la retenue et les bits de plus haut poids restent inchangés :
On remarque en particulier que le bit de plus haut poids de A+ est toujours égal à 1. Ce bit an peut donc être interprété comme un bit de signe : 0 pour les entiers positifs et 1 pour les entiers négatifs.
Considérons un entier positif A et son opposé B = −A. Nous pouvons écrire leur représentation binaire respective :
Compte tenu de notre convention nous obtenons la valeur de l'entier positif A en utilisant la somme classique sur les n bits de bas poids :
Comme la représentation binaire de B est le complément vrai de celle de A, nous pouvons écrire :
Soit encore :
C'est-à-dire :
ou
Donc :
En prenant en compte le bit de signe, nous pouvons rassembler les deux expressions précédentes donnant la valeur numérique associée à une représentation binaire en complément à deux sur n+1 bits sous une forme générale :
Ce codage nous permet de représenter 2n+1 nombres entiers compris entre −2n et 2n − 1.
d) Entiers en représentation biaisée
En binaire pur, avec n+1 bits nous pouvons représenter 2n+1 entiers compris entre 0 et 2n+1-1. Si nous soustrayons à chacun des nombres ainsi représentés la valeur médiane de cet intervalle, soit 2n, nous obtenons des entiers signés compris entre -2n et 2n - 1. Cela correspond à la représentation biaisée ou décalée. Pour n+1 bits le biais à soustraire est 2n :
En binaire pur, avec n+1 bits nous pouvons représenter 2n+1 entiers compris entre 0 et 2n+1-1. Si nous soustrayons à chacun des nombres ainsi représentés la valeur médiane de cet intervalle, soit 2n, nous obtenons des entiers signés compris entre -2n et 2n - 1. Cela correspond à la représentation biaisée ou décalée. Pour n+1 bits le biais à soustraire est 2n :
Nous pouvons remarquer que cette représentation est identique au complément vrai à une inversion de la convention du bit de signe près : 0 pour les valeurs négatives et 1 pour les valeurs positives. En effet l'expression précédente peut encore s'écrire :
En particulier, le bit de signe du zéro est également 1.
e) Nombres fractionnaires en virgule fixe
Pour le codage des entiers on attribue un poids 1 au bit de poids le plus faible. Si nous lui attribuons un poids 2-m avec n bits nous pouvons écrire :
Les m bits de poids faibles représentent la partie fractionnaire du nombre et les n−m bits de poids forts sa partie entière. La position de la virgule est fixée par le choix de m. Cette représentation est applicable aux représentations signées.
En valeur absolue la plus petite valeur représentée correspond à 2-m , et la grande à 2n-m(ou presque), soit une gamme dynamique (rapport entre ces deux valeurs extrêmes) de 2n.
f) Nombres en virgule flottante
En calcul scientifique on a souvent besoin de manipuler des nombres très grands ou très petits. Pour cela on utilise la notation exponentielle, sous la forme :
où M est la mantisse et E l'exposant. La précision de la représentation dépend du nombre de bits réservés à la mantisse. Les formats ont été, et sont encore, très variés selon les constructeurs et les processeurs. Il existe cependant des standards, comme la norme IEEE 754. Dans celle-ci la représentation en simple précision est codée sur 32 bits.
Ce format comporte le bit de signe de la mantisse (bit 31), suivi de n = 8 bits pour l'exposant en représentation biaisée (bits 23 à 30), puis de m = 23 bits pour la mantisse codée en virgule fixe (bits 0 à 22).
Sauf pour le zéro (codé par un mot nul : 000…0) nous pouvons toujours choisir l'exposant de telle façon que la mantisse soit comprise entre 0.5 et 1. Cela signifie que le bit de plus haut poids de la mantisse est toujours égal à 1 : la mantisse est dite normalisée. Ce bit peut être oublié (en particulier dans la norme IEEE 754), on gagne ainsi un bit pour la résolution. On dit alors que la mantisse est à bit caché. Le choix de la représentation biaisée pour l'exposant permet, dans ce cas, d'éviter toute confusion entre les représentations du zéro et du nombre 1/2. En effet 1/2 = 0,5 20. Le bit de signe de E = 0 en représentation biaisée étant 1, il y a un bit à 1 dans la représentation binaire avec mantisse à bit caché de 1/2.
La norme autorise de dénormaliser la mantisse pour représenter des nombres plus petits que 0.1 2-127
3 - Opérations arithmétiques et logiques
Le traitement des opérations logiques (ET, OU inclusif, NON, OU exclusif, etc…) est direct en électronique numérique. Outre ces fonctions logiques l'unité arithmétique et logique est chargée de l'exécution d'opérations arithmétiques comme addition, soustraction, décalage et multiplication. Nous avons déjà étudié le principe de l'additionneur-soustracteur. Etudions rapidement le principe de la multiplication.
La multiplication ou la division d'un entier non signé par une puissance de deux (2m) revient à effectuer un décalage de m cases respectivement vers la gauche ou la droite et à remplacer les cases "vides" par des 0. Considérons un entier non signé codé sur n bits :
Multiplions ce nombre par 2m :
Il faut donc n+m bits pour coder le résultat et nous pouvons écrire pour B :
Ainsi lorsqu'on multiplie deux nombres de n bits il peut falloir jusqu'à 2n bits pour contenir le résultat. Dans le cas des nombres signés en complément vrai il faut apporter une attention particulière au bit de signe. Avant la multiplication on procède à une extension de signe pour passer à 2n bits. C'est-à-dire qu'on recopie le bit de signe dans les n bits supplémentaires de haut poids (fig. 3).
Considérons en effet un entier signé A codé en complément vrai sur n bits :
et un nombre B obtenu à partir de A par extension de signe sur m bits (m > n) :
Vérifions que A et B représentent la même quantité algébrique.
Développons :
Ce que nous voulions montrer.
Considérons maintenant la multiplication par 2 d’un entier signé A codé sur n bits :
Le résultat nécessite donc n+1 bits et nous avons pour le codage de B :
Donc après extension du bit de signe une multiplication par une puissance de deux (2m) est réalisée en décalant de m cases vers la gauche le mot binaire et en injectant des 0 dans les m bits de bas poids. Cette technique conserve automatiquement le signe du résultat.
Réalisons la division entière (sans partie fractionnaire) par 2 d’un entier signé A :
Nous avons donc pour le codage de B sur n bits :
Pour une division il faut donc conserver et propager le bit de signe dans le décalage à droite :
La multiplication de deux entiers signés de n bits en complément vrai se ramène à une combinaison de décalages et d'additions et éventuellement une soustraction. En effet :
L'algorithme de Booth permet de réduire le nombre d'additions en repérant les séries de 0 et de 1. Dans le cas des zéros il n'y a que des décalages à effectuer. Dans le cas d'une série de 1 il suffit de se rappeler que :
Donc :
Les m−p+1 décalages et additions sont remplacés par deux décalages, une addition et une soustraction.
La figure 5 donne une représentation symbolique de l'ALU, comprenant deux opérandes en entrée A et B, une destination D = F(A, B), n lignes en entrée permettant de sélectionner la fonction F à exécuter, d’apporter un éventuel report de retenue et de synchroniser le fonctionnement de l'unité, ainsi que m sorties indiquant une éventuelle retenue (carry), un dépassement de capacité (overflow), un résultat négatif, nul ou positif, etc. Les opérandes et la destination sont toujours des registres.
Les premiers ordinateurs disposaient d'opérateurs spécifiques câblés. Aujourd'hui dans les ordinateurs modernes on trouve de moins en moins de circuits de ce type. Il n'existe par exemple plus de circuits propres à la multiplication ou à la division. L'enchaînement des actions à entreprendre pour réaliser une multiplication (décalages, additions et soustractions) est géré par l'unité de commande. Il en est de même pour le chargement des opérandes, la sélection des opérations à exécuter, etc.
4 - Réalisation d’un multiplieur
Nous nous intéressons dans ce paragraphe à la réalisation d’un multiplieur. Nous avons vu qu’une multiplication peut être obtenue par une succession d’additions et de décalages. Un tel multiplieur comprend une composante chargée de réaliser les opérations élémentaires et une logique de contrôle chargée d’enchaîner ces opérations. Cette étude nous donnera une vision simple des rôles respectifs de l’unité de calcul et de l’unité de commande d’un processeur.
Il existe de nombreuses manières d’implémenter un multiplieur, nous nous proposons ici de transposer le plus directement possible le processus que nous avons expliqué un peu plus haut. Dans un premier temps choisissons des composants permettant de réaliser cette multiplication. Si nous travaillons sur n bits nous savons que le résultat tiendra sur 2n bits. Il nous faut donc deux registres de 2n bits (R0 et R1) destinés à contenir respectivement le multiplicande et le multiplicateur. Ils doivent être chargés avec extension du bit de signe. Il nous faut également un additionneur de 2n bits et un registre de 2n bits (ACC) pour contenir le résultat des additions successives. Le registre contenant le multiplicande doit être un registre à décalage à gauche avec chargement série de 0 à droite. Le registre contenant le multiplicateur doit être un registre à
décalage à droite avec accès au contenu du bit de poids faible.
Explicitons sur un exemple la suite des opérations à réaliser. Travaillons avec n = 4 bits. Effectuons la multiplication suivante : 3 × −6 = −18. En binaire sur 4 bits, nous avons 3 = 0011 et −6 = 1010, ce qui nous donne après extension du bit de signe sur 8 bits 3 = 00000011 et −6 = 11111010.
Interprétons le résultat obtenu ACC = 11101110. Le bit de signe est 1, le résultat est donc négatif. Calculons sa valeur : ACC = 2 + 22 + 23 + 25 + 26 − 27 = −18. Nous obtenons bien le résultat correct. Remarquons que toutes les opérations ont été effectuées sur 2n bits sans tenir compte des débordements lors des décalages de R0 ni des retenues lors des additions. Nous avons introduit un compteur C pour compter les 2n itérations nécessaires. La figure 6 schématise l’organigramme du multiplieur. R10 correspond au bit le moins significatif du registre R1.
Faisons l’inventaire des signaux nécessaires pour commander le fonctionnement des cinq composants du multiplieur :
- registre ACC :
· remise à zéro : RAZ_ACC
· chargement : W_ACC
- registre R0 :
· chargement : W_R0
· décalage : D_R0
- registre R1 :
· chargement : W_R1
· décalage : D_R1
- additionneur :
· aucun signal
- compteur C :
· remise à zéro : RAZ_C
· incrémentation : I_C
Il nous faut maintenant étudier l’automate qui doit produire ces signaux. A partir de l’organigramme précédent nous pouvons identifier quatre états :
- Initialisation :
· RAZ_ACC = 1, W_ACC = 0
· W_R0 = 1, D_R0 = 0
· W_R1 = 1, D_R1 = 0
· RAZ_C = 1, I_C = 0
- Addition :
· RAZ_ACC = 0, W_ACC = 1
· W_R0 = 0, D_R0 = 0
· W_R1 = 0, D_R1 = 0
· RAZ_C = 0, I_C = 0
- Décalages et incrémentation :
· RAZ_ACC = 0, W_ACC = 0
· W_R0 = 0, D_R0 = 1
· W_R1 = 0, D_R1 = 1
· RAZ_C = 0, I_C = 1
- Opération terminée :
· RAZ_ACC = 0, W_ACC = 0
· W_R0 = 0, D_R0 = 0
· W_R1 = 0, D_R1 = 0
· RAZ_C = 0, I_C = 0
Nous constatons que nous pouvons limiter le nombre de signaux de commande en effet :
RAZ_ACC = W_R0 = W_R1 = RAZ_C
D_R0 = D_R1 = I_C
Par contre nous avons besoin d’un signal supplémentaire pour indiquer à l’extérieur que l’opération est terminée ou non. L’automate doit donc produire quatre signaux de commande que nous notons INIT, W_ACC, ITER et FIN, avec :
RAZ_ACC = W_R0 = W_R1 = RAZ_C = INIT
D_R0 = D_R1 = I_C = ITER
Pour identifier quatre états différents nous avons besoin de 2 variables que nous notons Q0 et Q1. Nous choisissons la convention suivante :
A partir de cette table 3, il est très facile d’exprimer les quatre signaux de commande à partir des variables d’état. Il nous suffit donc de construire ces deux variables d’état. Pour cela nous devons tenir compte du bit le moins significatif du registre R1 (R10) et d’un autre signal indiquant que le compteur a atteint la valeur maximale 2n que nous notons C_max. Par convention nous choisissons C_max = 1 pour indiquer que le compteur est égal à 2n.
Nous avons pour les signaux de commande :
La table précédente résume les diverses transitions que peut subir l’automate de contrôle. Les variables Q et
Q+ correspondent respectivement aux états avant et après la transition. Nous avons repéré plusieurs configurations impossibles :
- Q0 = Q1 = 1 (terminé) et C_max = 0, alors que pour passer dans l’état terminé il faut que le compteur ait atteint sa valeur maximale.
- Q0 = Q1 = 0 (initialisation) et C_max = 1, alors que la phase d’initialisation met à zéro le compteur.
- Q0 = 1 et Q1 = 0 (addition) et C_max = 1, si le compteur a atteint sa valeur maximale l’automate passe dans l’état terminé, pas addition.
Utilisons des tableaux de Karnaugh, présentés figure 7, pour déterminer les expressions logiques de Q0+ et Q1+ .
Nous devons synchroniser l’automate sur un signal externe d’horloge H. Ainsi nous pouvons utiliser des bascules, par exemple D, pour réaliser les variables d’état. Dans ce cas nous aurons Q+ = D. Donc :
Dans cette première phase de notre étude nous avons oublié qu’un signal extérieur, que nous notons Start, est nécessaire pour lancer l’opération. Ce signal ne doit avoir d’effet (par exemple dans l’état Start = 1) que lorsque l’automate de contrôle est dans l’état "Opération terminée". Il doit alors le faire passer dans l’état "Initialisation". Une façon simple de tenir compte de cette contrainte est de construire les fonctions D0 et D1 en utilisant la variable Start • FIN. La table 4 et les tableaux de Karnaugh de la figure 7 restent valables lorsque Start • FIN = 0. Lorsque Start • FIN = 1, l’automate est nécessairement dans l’état Q0 = Q1 = 1
(pour avoir FIN = 1) et doit passer dans l’état Q0 = Q1 = 0. Les tableaux de Karnaugh permettant de déterminer les fonctions D0 et D1 sont alors identiques et correspondent au tableau figure 8. La simplification globale de ces tableaux de Karnaugh nous conduit aux expressions suivantes :
Le logigramme du circuit multiplieur que nous venons de concevoir est représenté sur la figure 9.
5 - Unité de commande
Revenons à l’étude des processeurs. L'unité de commande dirige le fonctionnement de tous les autres éléments de l'unité centrale en leur envoyant des signaux de commande. Les principaux éléments de l'unité de commande sont :
- le compteur ordinal (CO) : registre contenant l'adresse en mémoire où se trouve l'instruction à chercher;
- le registre instruction (RI) qui reçoit l'instruction qui doit être exécutée;
- le décodeur qui détermine l'opération à effectuer et les opérandes;
- le séquenceur qui génère les signaux de commande aux différents composants;
- l'horloge (interne ou externe) qui émet des impulsions permettant la synchronisation de tous les éléments de l'unité centrale.
Une horloge est un système logique, piloté par un oscillateur, qui émet périodiquement une série d'impulsions calibrées. Ces signaux périodiques constituent le cycle de base ou cycle machine. Nous avons déjà vu (dans le premier chapitre) les différentes phases de l'exécution d'une instruction. Un cycle d'instruction peut se décomposer en un cycle de recherche (instruction et opérandes) et un cycle d'exécution. On rencontre parfois le terme de cycle cpu pour indiquer le temps d'exécution de l'instruction la plus courte.
N'oublions cependant pas que les performances d'un ordinateur ne dépendent pas de la seule cadence de l'unité centrale. Elles dépendent également des mémoires et des bus, ainsi que de l'architecture, avec par exemple l'utilisation d'antémémoire (mémoire cache) pour anticiper les transferts des instructions et des données.
6 - Technologie des circuits intégrés et horloge
L'oscillateur fournissant le signal d'horloge peut être intégré sur la puce silicium du processeur. Ce n'est généralement pas le cas, pour au moins deux raisons.
Tout d'abord, la fréquence d'oscillation est sensible à la température. Or la température d'un processeur peut varier en fonction de son utilisation. Il serait possible d'observer une dérive fatale, la fréquence augmentant avec la température et la température augmentant avec la vitesse de fonctionnement. Cela poserait également des problèmes de synchronisation avec les composants externes au CPU.
Par ailleurs en embarquant une horloge dans la puce du processeur la fréquence de celui-ci serait figée par construction. Or les galettes de silicium ne sont jamais parfaitement homogènes. Les performances peuvent varier selon les zones. Le constructeur serait alors obligé d'ajuster la fréquence de l'oscillateur au plus bas, en prenant un facteur de sécurité. Alors qu'actuellement, les processeurs sont triés et vendus à un prix variant selon leur vitesse de fonctionnement.
On préfère donc un oscillateur interne synchronisé sur un signal d'horloge externe, souvent fourni par un oscillateur à quartz. Nous étudierons un peu plus loin ce système de synchronisation, basé sur une boucle à verrouillage de phase, dont les applications sont nombreuses dans les ordinateurs : horloge CPU, enregistrement et lecture de données sur disque dur ou disque optique, transmission de données, etc.
Mais commençons par résumer succinctement le processus de fabrication des circuits intégrés et des processeurs en particulier.
a) Fabrication d’un circuit intégré
L’électronique repose sur l’emploi de semi-conducteurs tels que le silicium (Si) ou le germanium (Ge). Ces deux éléments appartiennent à la même colonne de la classification périodique que le carbone. Ils possèdent donc quatre électrons de valence et ont une structure cristalline analogue à celle du diamant : chaque atome échange quatre liaisons covalentes avec quatre atomes placés aux sommets d’un tétraèdre régulier. La figure 10 donne une représentation symbolique en deux dimensions d’un cristal pur. A la température ambiante quelques liaisons covalentes peuvent être brisées libérant chacune un électron qui peut participer à la conduction. D’autre part, l’absence d’un électron dans une liaison covalente constitue un trou. Les trous contribuent également à la conduction. Qualitativement le mécanisme de déplacement d’un trou
est le suivant : lorsqu’un trou existe, il est assez facile pour un électron de valence voisin de quitter son orbitale pour venir combler le trou. L’électron laisse un trou au niveau de l’atome qu’il a quitté. Ce trou peut à nouveau être comblé par un autre électron et ainsi de suite. Le mouvement apparent de ce trou est équivalent au déplacement d’un charge positive. La conduction sous ces deux types de porteurs (électrons et trous) nécessite la continuité du réseau cristallin. Les circuits sont réalisés à partir d’un monocristal.
Dans un cristal pur (intrinsèque) les densités de porteurs sont trop faibles. Il est nécessaire d’introduire, sans perturber la structure du réseau cristallin, des dopants : des impuretés d’atomes trivalents ou pentavalents. L’introduction d’une impureté de valence cinq (antimoine, phosphore ou arsenic) apporte un électron en excès très faiblement lié qui contribue facilement à la conduction. Ces impuretés de type n sont appelés donneurs. Inversement l’introduction d’impuretés de valence trois (bore, gallium ou indium), dites accepteurs, produit des semi-conducteurs de type p pour lesquels les porteurs majoritaires sont des trous.
Les portes logiques sont réalisées à partir de transistors qui sont obtenus en combinant des zones comportant différents dopants. La figure 12 présente par exemple un transistor MOS (Métal – Oxyde - Silicium) de type n. Un tel transistor peut être utilisé comme un interrupteur commandé. Si la grille G est soumise à une tension positive elle attire des électrons qui comblent les trous du semi-conducteur de type p puis provoquent une inversion de population et créent un canal n induit. La conduction est alors possible entre la source S et le drain D. Un circuit intégré est constitué d’un très grand nombre de transistors réalisés en dopant des zones très précises et interconnectés.
La fabrication des circuits intégrés commence par la production d’un monocristal sans défaut ultra pur. Ce lingot est obtenu à partir d’un germe plongé dans un bain de silicium fondu maintenu à une température très proche du point de fusion (1400 °C) sous une atmosphère d’argon. Le germe tourne régulièrement pendant qu’il est remonté lentement. On obtient ainsi un cylindre de 6 ou 8 pouces de diamètre. Dans quelque temps on devrait atteindre 12 et 16 pouces. Le lingot est ensuite découpé en très fines tranches ou galettes (environ 500-600 µm d'épaisseur). Ces galettes sont ensuite polies mécaniquement et chimiquement.
Pour réaliser les transistors, les résistances, les condensateurs et les connexions il faut doper certaines zones avec des impuretés de type donneur ou accepteur et avec différentes concentrations. Pour cela on procède par couches superposées. Différentes techniques sont utilisées pour déposer, faire croître ou diffuser ces implants. Certaines couches doivent être séparées par une couche de dioxyde de silicium pour isolation (1500 Å) ou protégées (passivation : 200-500 Å). Cette couche d’oxyde est obtenue par exposition de la galette à une atmosphère d’oxygène et d’hydrogène de haute pureté à environ 1000 °C.
Dans tous les cas il faut délimiter en surface les zones à traiter. Pour cela on utilise un masque gravé sur un réticule. L'image, à l’échelle 5 à 10, est tracée au laser dans une fine couche de chrome déposée sur une plaquette de quartz. Par ailleurs, la galette est recouverte d'une pellicule de résine photorésistive, dont il existe deux types : négative ou positive. Au moyen d’un système optique sophistiqué le masque et la galette sont exposés à un rayonnement laser ultraviolet. La résine (positive) exposée subit une transformation chimique et devient acide. Puis un révélateur basique retire la résine exposée. Le traitement (attaque chimique, dopage par bombardement ionique, dépôt métallique ou épitaxie) peut alors être réalisé, puis le reste de la résine est retiré à l'aide d'un solvant. On répète ces opérations quelques dizaines de fois, entre chaque étape la galette est rincée à l’eau ultra pure.
Les procédures de gravure des masques et d’insolation gouvernent la finesse du dessin des composants. Actuellement les constructeurs travaillent un pas de 0.13 µm. Il semble cependant qu'on approche des limites technologiques de la gravure. La finesse du tracé de la gravure est principalement limitée par la longueur d'onde de la source lumineuse utilisée pour l'insolation. Il faut en particulier limiter les phénomènes de diffraction. Les rayons X ou les électrons pourraient être employés dans un avenir proche. On prévoit un pas de 22 nm vers 2015. Au-delà la nanoélectronique est encore du domaine du laboratoire.
Sur une galette on réalise un grand nombre de circuits. Ceux-ci sont tous testés et marqués avant que la galette ne soit découpée en plaquettes avec une scie au diamant. Chaque plaquette est ensuite placée sur un support et les connexions avec les contacts extérieurs sont réalisés par des fils d'aluminium ou d'or de 30 µm de diamètre, ou à l’aide de micro-billes de soudure. L'ensemble est ensuite enfermé dans un boîtier en plastique ou en céramique.
b) Boucle à verrouillage de phase
Nous ne présentons ici que le principe, très schématisé, du fonctionnement d'une boucle à verrouillage de phase (PLL : Phase Locked Loop). La structure minimale consiste en une boucle de rétroaction contenant :
- un comparateur de phase;
- un oscillateur commandé en tension.
On trouve de nombreuses utilisations des PLL dans les ordinateurs : horloge CPU, enregistrement et lecture de données sur disque dur ou disque optique, transmission de données, etc.
Le comparateur de phase est un circuit fournissant une tension dont la valeur dépend de la différence de phase entre deux signaux périodiques. Nous illustrons notre analyse en supposant les signaux sinusoïdaux. Mais cela ne retire rien à la généralité de l'étude puisque tout signal périodique, comme un signal d’horloge, peut être décomposé en une série de Fourier :
Donc par définition, la tension à la sortie du comparateur de phase peut se mettre sous la forme :
où f est une fonction de période 2 π. Nous supposons que les amplitudes S1 et S2 sont constantes.
Pour simplifier les notations, en nous limitant aux termes importants, nous prenons S1 = S2 = 1, ce qui nous donne :
Cette tension est utilisée pour commander l'oscillateur. L'oscillateur commandé en tension (VCO : Voltage Controlled Oscillator) délivre un signal, ici sinusoïdal, dont la pulsation instantanée est une fonction linéaire de la tension de commande. C'est-à-dire :
Si nous explicitons la tension de commande fournie par le comparateur de phase dans cette expression il vient :
Dérivons cette expression par rapport au temps :
Nous notons kϕ la sensibilité du comparateur de phase, définie par :
L'équation différentielle peut alors s'écrire :
Soit :
La solution de cette équation différentielle peut se mettre sous la forme d'une somme de deux
termes :
- le régime transitoire : solution générale de l'équation sans second membre;
- le régime permanent : solution particulière de l'équation complète.
Si nous avons pour le signal s1 une pulsation constante :
nous pouvons essayer une solution particulière telle que :
Il vient alors :
C'est-à-dire que les deux phases sont égales à une constante additive près :
La pulsation du signal en sortie du VCO est donc égale à celle du signal s1 et le déphasage entre les deux signaux est fixe :
Ainsi, après une phase transitoire, la boucle s'accroche ou se verrouille. Le déphase entre les deux signaux est tel que la tension de commande permet d'obtenir une pulsation identique à celle du signal de référence.
Ce qui nous donne pour le déphasage :
Nous avons simplifié la résolution de l'équation différentielle en supposant la sensibilité du comparateur kϕ constante. Si ce n'est pas le cas, cela ne change rien au régime permanent. Par contre cela peut influer sur le régime transitoire et en particulier sur les conditions d'accrochage de la boucle.
c) Multiplicateur de fréquence
Cependant la transmission d'un signal d'horloge de très haute fréquence pose de nombreux problèmes techniques. Pour ne pas limiter la fréquence de fonctionnement de l'unité centrale à celle de ce signal externe on utilise un multiplicateur de fréquence.
Il s'agit en fait d'un diviseur de fréquence, par exemple un compteur, placé dans la contre-réaction de la boucle à verrouillage de phase.
Si celui-ci divise la fréquence ω par n. La boucle est donc verrouillée si :
C'est-à-dire que l'oscillateur commandé émet un signal avec une fréquence n fois celle du signal de référence. Ce coefficient de multiplication n est chargé dans l'unité centrale lorsque celle-ci est initialisée.
d) Fréquence d'horloge, gravure et puissance dissipée
L'augmentation de la fréquence d'un processeur pose quelques problèmes techniques, en particulier au niveau de la puissance thermique dissipée et des perturbations électromagnétiques. Plus un circuit fonctionne rapidement, plus les intensités des courants, et donc la puissance consommée, sont élevées. Une façon de réduire cet inconvénient consiste à utiliser une tension d'alimentation plus faible, par exemple 3.3 V au lieu de 5 V. Par ailleurs plus les signaux sont rapides plus ils induisent, par couplage capacitif, des parasites dans leur voisinage. En baissant la tension on diminue l'amplitude de ces parasites, mais on augmente la sensibilité du circuit aux parasites externes.
L'augmentation de la densité d'intégration fournit également des réponses à ces difficultés. La réduction du pas de la gravure présente de nombreux avantages. Cela permet évidemment de diminuer la surface de silicium utilisée, un gain d'un facteur 2 sur la gravure réduit la surface par 4. Il est alors possible :
- soit d'augmenter les fonctionnalités pour une même surface de silicium;
- soit de diminuer la surface de silicium, donc le coût, à fonctionnalités constantes.
Par ailleurs, cela permet une diminution du temps de transit des signaux et une diminution des intensités, donc une réduction de la puissance dissipée. Ces deux derniers avantages permettent donc augmenter la vitesse de fonctionnement. Par contre, la diminution de la surface de silicium rend l'évacuation de la chaleur plus difficile. Il faut faire appel à de la graisse ou de la pâte thermique pour assurer une bonne conduction entre la puce et le ventilateur, ou encore utiliser un refroidissement par plaque à effet Peltier.
7 - Séquenceur
Le séquenceur est un automate distribuant, selon un chronogramme précis, des signaux de commande aux diverses unités participant à l'exécution d'une instruction. Il peut être câblé ou microprogrammé.
Un séquenceur câblé est un circuit séquentiel complexe comprenant un sous-circuit pour chacune des instructions à commander. Ce sous-circuit est activé par le décodeur.
De même pour reproduire une séquence d'opérations élémentaires il suffit d'un mot par "tranche" de temps. Cette série de mots constitue un microprogramme. Le code opération de l'instruction à exécuter peut être utilisé pour définir le pointeur sur la première micro-instruction du microprogramme. En fonction du code opération le contenu d'un compteur est initialisé, puis celui-ci s'incrémente ensuite à chaque cycle d'horloge. La période de l'horloge utilisée à ce niveau peut être plus élevée que celle qui règle la cadence des autres éléments de l'unité centrale. Ce compteur sert à adresser une mémoire morte. La figure suivante illustre ce principe :
Le format des micro-instructions varie selon les machines. Le schéma de la figure 16 correspond à celui proposé initialement par Wilkes avec des micro-instructions longues où chaque bit correspond à une ligne de commande. On parle alors de microprogrammation horizontale. A l'extrême une autre solution consiste à utiliser des micro-instructions compactes nécessitant un décodage avant la génération des signaux de commande. La microprogrammation est alors dite verticale. En microprogrammation horizontale la mémoire de commande comprend peu de micro-instructions, chacune comptant un grand nombre de bits. En microprogrammation verticale la longueur des micro-instructions est plus courte mais il y a un plus grand nombre de micro-instructions et il faut un décodage supplémentaire. Dans la pratique on rencontre des
micro-instructions mixtes pour lesquelles certains bits agissent directement sur les lignes de commande associées alors que d'autres champs nécessitent un décodage. Un microprogramme peut également contenir des boucles, des tests et des ruptures de séquence. Le compteur est alors remplacé par un micro-séquenceur.
Intrinsèquement un séquenceur microprogrammé est plus lent qu'un séquenceur câblé. L'avantage et les gains en performance d'un séquenceur microprogrammé résident dans la simplicité de sa conception et la souplesse de son utilisation. Il est ainsi possible d'offrir un jeu d'instructions très complexes. Une instruction peut donc être équivalente à plusieurs instructions d'une autre machine. On gagne alors sur le temps de transfert des instructions. Par ailleurs cela permet une plus grande souplesse aux compilateurs de haut niveau pour optimiser le code objet. Il est également possible d'augmenter le nombre d'instructions sans augmenter la complexité, donc le coût, du processeur. Nous avons ici un premier exemple de l'imbrication du matériel et du logiciel dans la conception d'une architecture.
Pour programmer un ordinateur on utilise généralement des langages dits évolués ou de haut niveau : C, C++, Java, Basic, Fortran, Pascal, Ada, Assembleur, etc. Cependant l'unité centrale ne peut exploiter que les instructions machine : les codes binaires qui sont chargés dans le registre instruction.
Le terme de langage désigne un jeu d'instructions et de règles syntaxiques. A l'aide d'un langage évolué le programmeur écrit un code source. Celui-ci n'est pas directement exécutable par l'ordinateur. Il faut le traduire en code machine ou code objet. C'est le rôle des compilateurs ou assembleurs et des interpréteurs. Un interpréteur ne produit pas de code objet il traduit les instructions directement au fur et à mesure de l'exécution du programme.
La figure 17 schématise les différents niveaux de programmation. Lorsque l'utilisateur peut accéder au niveau de la micro-programmation la machine est dite micro-programmable.
8 - Registres de l'unité centrale
Le nombre et le type des registres implantés dans une unité centrale font partie de son architecture et ont une influence importante sur la programmation et les performances de la machine. Nous voudrions ici passer en revue les registres fondamentaux, que l'on retrouve sur toutes les machines ou presque.
Compteur ordinal (CO) : Ce registre (Program Counter : PC) contient l'adresse de la prochaine instruction à exécuter. Après chaque utilisation il est automatiquement incrémenté du nombre de mots correspondant à la longueur de l'instruction traitée : le programme est exécuté en séquence. En cas de rupture de séquence (branchement conditionnel ou non, appel à une routine, etc.) il est chargé avec la nouvelle adresse. Le compteur ordinal, dont la taille dépend de l'espace adressable, n'est généralement pas accessible directement au programmeur.
Registre instruction (RI) : C'est le registre de destination dans lequel le CPU transfert l'instruction suivante à partir de la mémoire. Sa taille dépend du format des instructions machines. Le décodeur utilise le registre instruction pour identifier l'action (ou le micro-programme) à entreprendre ainsi que les adresses des opérandes, de destination ou de saut. Le programmeur n'a pas accès au registre instruction.
Accumulateur (ACC) : L'accumulateur est un registre de l'unité arithmétique et logique. Il a de nombreuses fonctions. Il peut contenir un des deux opérandes avant l'exécution et recevoir le résultat après. Cela permet d'enchaîner des opérations. Il peut servir de registre tampon pour les opérations d'entrées/sorties : dans certaines machines c'est le seul registre par lequel on peut échanger des données directement avec la mémoire. Sa taille est égale à la longueur des mots en mémoire. Il possède souvent une extension (Q), pour les multiplications, décalages, divisions, etc. Le registre ACC est accessible au programmeur et très sollicité. Certaines machines possèdent plusieurs accumulateurs.
Registres généraux ou banalisés : Ils permettent de limiter les accès à la mémoire, ce qui accélère l'exécution d'un programme. Ils peuvent conserver des informations utilisées fréquemment, des résultats intermédiaires, etc. Ils sont accessibles au programmeur.
Registres d'indice ou d'index : (XR) Ils peuvent être utilisés comme des registres généraux mais ils ont une fonction spéciale utilisée pour l'adressage indexé. Dans ce cas l'adresse effective d'un opérande est obtenue en ajoutant le contenu du registre d'index à l'adresse contenue dans l'instruction. Ce type d'adressage et de registre est très utile pour manipuler des tableaux. Le programmeur dispose alors d'instructions permettant l'incrémentation ou la décrémentation du registre d'index. En particulier les registres d'index peuvent être incrémentés ou décrémentés automatiquement après chaque utilisation. Dans certaines machines ces instructions sont applicables à tous les registres généraux, il n'y a alors pas de registre d'index spécifique.
Registre de base : A de très rares exceptions à l'intérieur d'un programme on ne fait référence qu'à des adresses relatives ou virtuelles. Par contre l'unité centrale a besoin de connaître les adresses physiques où se situent réellement instructions et données. Celles-ci dépendent de l'endroit où a été chargé le programme en mémoire, l'espace physique occupé par un programme pouvant ne pas être contigu. Le rôle des registres de base est de permettre le calcul des adresses effectives. Un registre de base contient une adresse de référence, par exemple l'adresse physique correspondant à l'adresse virtuelle 0. L'adresse physique est obtenue en ajoutant au champ adresse de l'instruction le contenu du registre de base. Le registre de base est encore utilisé quand le nombre de bits du champ adresse ne permet pas d'accéder à toute la mémoire.
Registre d'état (RE ou PSW : Program Status Word) : Une partie des bits de ce registre, aussi appelé registre condition, constitue des drapeaux (flags) qui indiquent certains états particuliers. Par exemple à la fin de chaque opération on peut y trouver le signe du résultat (Négatif, Zéro ou Positif), ainsi qu'une éventuelle retenue (Carry) ou un dépassement de capacité (Overflow). Ces bits indicateurs peuvent être testés pour déterminer la suite du déroulement du programme : branchements conditionnels. On trouve également le mode de fonctionnement de l'unité centrale. Deux modes sont possibles le mode utilisateur et le mode système ou superviseur. Dans le mode utilisateur certaines instructions sont interdites : elles provoquent un déroutement vers le système d'exploitation. Un bit peut également indiquer un déroulement pas à pas : emande de trace (T). Le registre peut aussi contenir le niveau de l'interruption en cours de traitement ou un masque des niveaux d'interruptions autorisés.
Registre pointeur de pile (PP) : Une pile est une zone mémoire dans laquelle les informations sont rangées de façon contiguë. L’usage d’une pile permet la récursivité des appels à des routines ou fonctions. Elle sert à sauvegarder l’adresse de retour, les registres qui sont utilisés par la fonction appelée. Elle peut également servir au passage direct ou indirect des arguments. Le pointeur de pile (Stack Pointer : SP) indique le sommet de la pile : la position de la dernière information enregistrée. Dans certaines machines le pointeur de pile indique la position où sera mémorisée la prochaine donnée. Le fonctionnement d'une pile est du type
Dernier Entré Premier Sorti (LIFO : Last In First Out). Les deux principales opérations liées à la pile concernent l'ajout d'un élément dans la pile ou le retrait, souvent nommées respectivement PUSH et PULL. Lorsqu'une donnée est enregistrée dans la pile elle est placée à l'adresse qui suit celle du dernier mot stocké. Après l'opération le pointeur de pile est incrémenté. Lorsque un mot est retiré de la pile il correspond à la dernière information qui y a été entrée. Après l'opération le pointeur est décrémenté. Une pile est réservée à l'usage de l'unité centrale, en particulier pour sauvegarder les registres et l'adresse de retour en cas d'interruption ou lors de l'appel d'une procédure. Le pointeur de pile est accessible au programmeur, ce qui est souvent source d'erreur. Certaines machines sont dotées de plusieurs pointeurs de piles.
Pour améliorer les performances d'un processeur il faut disposer du plus grand nombre de registres possible. On réduit ainsi les accès à la mémoire. De plus, il est préférable d'éviter de les spécialiser. On évite ainsi des transferts entre registres, par exemple pour calculer la valeur d'un indice et utiliser ensuite cet indice pour modifier une case d'un tableau.
9 - Structures des instructions au niveau machine
a) Format des instructions
Les ordinateurs sont capables d'effectuer un certain nombre d'opérations élémentaires. Une instruction au niveau machine doit fournir à l'unité centrale toutes les informations nécessaires pour déclencher une telle opération élémentaire : type d'action, où trouver le ou les opérandes, où ranger le résultat, etc. C'est pourquoi une instruction comporte en général plusieurs champs ou groupes de bits. Le premier champ contient le code opération. Les autres champs peuvent comporter des données ou l'identification des opérandes. La figure 18 donne quelques exemples d'instructions à n adresses, pour n = 0, 1 et 2. Sur certaines machines les instructions sont toutes de même longueur, sur d'autres cette longueur peut varier avec le code opération ou le mode d'adressage.
On distingue six groupes d'instructions :
- transferts de données : de mémoire à registre, de registre à registre, de registre à mémoire;
- opérations arithmétiques : addition, soustraction, multiplication et division;
- opérations logiques : ET, OU inclusif, NON, OU exclusif, etc.;
- contrôle de séquence : branchements conditionnels ou non, appel de procédure, etc.;
- entrées/sorties;
- manipulations diverses : décalage, conversion de format, permutation circulaire des bits, échange d'octets, incrémentation, etc.
Le choix de la longueur et du format des instructions est une étape très importante dans la conception d'une nouvelle architecture. C'est encore une affaire de compromis. La longueur des instructions se répercute sur la dimension de la mémoire centrale donc sur le coût : il faut deux fois plus de bits pour stocker un programme de n instructions de 32 bits qu'un programme de n instructions de 16 bits. La longueur des instructions par rapport à celle du mot mémoire influence également le temps de traitement : il faut tenir compte du temps de transfert des mots qui constituent une instruction. Ce choix dépend des vitesses relatives d'accès mémoire et de traitement effectif par l'unité centrale. Le temps de recherche doit être minimisé pour les processeurs très rapides.
La largeur en bits de chacun des différents champs est également importante, en particulier pour le code opération. Le nombre de bits est déterminé par le nombre d'opérations distinctes envisagées : n bits autorisent
2n instructions. Cependant toutes les opérations ne nécessitent pas forcément le même nombre de champs ou des champs de même longueur. Ainsi sur une machine même pour une longueur d'instruction donnée le format des instructions peut ne pas être fixe. Il peut dépendre du type d'opération. Pour illustrer le concept du code opération expansif imaginons des instructions de 16 bits découpées en quatre champs de 4 bits (fig. 19). Avec ce format nous pouvons définir 16 instructions à 3 adresses. C'est peu et toutes les instructions ne nécessitent pas trois adresses. Nous pouvons également définir 15 instructions à 3
adresses (code opération 0000 à 1110 dans le premier champ), 14 instructions à 2 adresses (code opération sur 8 bits 1111 0000 à 1111 1101 identifié par les quatre premiers bits à 1), 31 instructions à 1 adresse (code opération sur 12 bits 1111 1110 0000 à 1111 1111 1110 identifié par les sept premiers bits à 1) et 16 instructions sans champ adresse (identifiée par les douze premiers bits à 1). Soit un total de 76 instructions. Dans d'autres variantes la longueur et le format des instructions sont définis par les premiers bits du code.
D'autre part comme la capacité mémoire ne cesse de croître les champs d'adresse demandent de plus en plus de bits. C'est pourquoi, pour éviter une inflation de certains registres comme le registre instruction, aujourd'hui on préfère les instructions à une adresse. On peut par exemple faire en sorte qu'un des opérandes soit toujours l'accumulateur et que ce même registre recueille le résultat.
b) Modes d'adressage
Un champ adresse peut permettre de référencer un registre ou un mot en mémoire. Il peut contenir le numéro du registre ou l'adresse effective du mot mais ce ne sont pas les seules manières d'identifier un opérande. Pour faciliter la programmation il existe de nombreux modes d'adressage. Le mode est défini soit par le code opération lorsque celui-ci impose un type déterminé, soit par un code faisant partie du champ adresse.
Les exemples ci-dessous sont empruntés aux instructions de l'assembleur PDP-11.
Adressage implicite : Le code opération identifie automatiquement l'opérande, l'instruction ne peut porter que sur un registre particulier. Par exemple, le test sur le signe du résultat d'une opération arithmétique concerne le registre d'état RE. Dans certaines architectures les transferts avec la mémoire ne se font qu’à partir ou à destination du registre d’accumulation. Dans ces cas aucun champ adresse n'est nécessaire.
Adressage immédiat : La valeur de l'opérande est contenue dans le champ adresse si le nombre de bits dans ce champ est suffisant, sinon dans le mot suivant l'instruction.
Après cette instruction le registre R1 contient la valeur 100.
Adressage registre : Le champ adresse contient le numéro du registre opérande.
Après cette instruction le contenu de R3 est nul.
Adressage direct : Le champ adresse de l'instruction (ou le mot suivant si le nombre de bits n'est pas suffisant) contient l'adresse effective de l'opérande.
Après cette instruction le registre R2 contient le mot qui se situe à l'adresse 100 en mémoire, c'est-à-dire 250.
Adressage indirect : Le champ adresse (ou le mot suivant) contient l'adresse d'un pointeur : mot en mémoire qui contient l'adresse effective de l'opérande.
MOV (R1), R4
Après cette instruction R4 contient la valeur du mot dont l'adresse est contenue dans R1. Comme R1 vaut 100 on trouve 250 dans R4.
Adressage indexé : Ce mode d'adressage est très utile lorsqu'on travaille, par exemple, sur des tableaux. Considérons un bloc de n mots consécutifs débutant à l'adresse A. Le kième mot se
trouve à l'adresse A + (k − 1). Pour référencer ce mot il est possible d'utiliser un registre d'index. L'adresse effective est calculée en additionnant le contenu de ce registre d'index à l'adresse qui se trouve dans le champ adresse de l'instruction. Sur certaines machines tous les registres généraux peuvent être utilisés comme registres d'index. La présence d'un registre d'index s'accompagne généralement de la possibilité d'incrémentation et décrémentation automatiques.
MOV R4, 100(R3)+
CLR 100(R3)
Avant la première opération R3 est nul, donc le contenu de R4 est transféré à l'adresse 100. Après le registre R3 est incrémenté. L'instruction suivante permet de mettre à zéro le contenu du mot à
l'adresse suivante.
Adressage basé : L'adressage basé est comparable à l'adressage indexé mais cette fois l'adresse effective est obtenue en additionnant le contenu du registre de base au contenu du champ adresse de l'instruction. Ce mode d'adressage est utilisé par exemple en cas d'allocation dynamique de la mémoire : la position du programme en mémoire peut changer en fonction de la charge du système et il n'occupe pas toujours un espace contigu. Cette technique permet également de réduire le nombre de bits dans le champ adresse : le registre de base contient la première adresse d'un bloc de 2k mots et l'adresse (sur k bits) contenue dans l'instruction représente le déplacement à l'intérieur du bloc.
Adressage relatif : L'adresse effective est obtenue est additionnant le contenu du compteur ordinal au contenu du champ adresse de l'instruction. Ce type d'adressage est utilisé par exemple dans des instructions de branchement.
N'oublions pas que le calcul de l'adresse effective peut nécessiter quelques opérations (addition par exemple). L'utilisation de certains modes d'adressage sophistiqués (le 68020 de Motorola dispose par exemple d'une cinquantaine de modes d'adressage) peut donc augmenter le temps de traitement d'une instruction.
10 - Réalisation d’un multiplieur micro-programmé
Reprenons le multiplieur que nous avons étudié plus haut (§ VII.4). Il est basé sur une unité d’exécution et une unité de commande câblée. Nous voulons conserver l’unité d’exécution constituée de trois registres R0, R1 et ACC, un additionneur et un compteur. Le fonctionnement de cette unité est contrôlé par quatre signaux INIT, W_ACC, ITER et FIN, qui dépendent de deux signaux d’information R10 et C_max. Nous voulons remplacer l’automate de contrôle-commande par l’équivalent d’un séquenceur micro-programmé. Pour cela nous traduisons l’organigramme de la figure 6 en un micro-programme en pseudo-langage. L’exemple suivant se comprend aisément :
Nous n’avons ici que deux types d’instructions : des actions et un branchement conditionnel. Il suffit donc d’un bit pour identifier ce type, choisissons 0 pour les actions et 1 pour le branchement conditionnel.
Nous avons quatre actions (INIT, ADD, ITER et STOP) il nous faut donc deux bits pour les identifier. Ces instructions s’adressent implicitement à des éléments fonctionnels, nous n’avons donc pas besoin de champ supplémentaire.
Pour un branchement conditionnel il faut identifier la condition et l’adresse de saut. Il y a deux tests différents un bit est donc suffisant. Le micro-programme compte six instructions, il faut donc trois bits d’adresse. La longueur minimale d’une micro-instruction est donc cinq bit. Nous choisissons le format suivant, qui dépend du bit le plus significatif (bit 4) indiquant le type d’instruction.
Action :
- bit 4 : 0
- bits 3 et 2 : 00 INIT
01 ADD
10 ITER
11 STOP
- bits 0 et 1 : 00 (inutilisés)
Branchement conditionnel :
- bit 4 : 1
- bit 3 : 0 test sur R10
101 test sur C_max
- bits 0 à 2 : adresse de saut
Nous pouvons traduire le micro-programme en binaire en utilisant cette convention :
Nous devons concevoir le circuit de commande destiné à exploiter ce micro-programme. Nous avons besoin d’une mémoire d’au moins 6 mots de 5 bits, d’un compteur pour adresser cette mémoire et d’un registre de 5 bits pour contenir la micro-instruction courante.
Il nous faut un transcodeur pour produire les signaux de commande à partir des deux bits du champ action. Pour cela il est possible d’utiliser un démultiplexeur (fig. 21).
Lors d’un test positif le compteur doit être chargé à partir du champ adresse. La commande de chargement parallèle correspond donc à l’expression logique suivante :
Chrgt //= Op Condition
où Op représente le type d’instruction (bit 4 du registre micro-instruction) et Condition le signal indiquant si la condition du test est réalisée :
µr3 est le bit 3 du registre micro-instruction. Dans les autres cas le compteur doit être incrémenter d’une unité. Le comptage doit être bloqué lorsque la multiplication est terminée, pour cela nous pouvons employer le signal fin. Ce qui nous donne :
Le signal extérieur Start de démarrage de la multiplication, si l’opération précédente est terminée, doit faire une remise à zéro du compteur pour relancer le micro-programme à l’instruction INIT. Nous avons simplifié la lecture de la mémoire micro-programme en supposant que l’affichage de l’adresse suffisait à transférer la micro-instruction courante dans le registre.
11 - Traitement anticipé des instructions : pipeline
Nous avons vu que le traitement d'une instruction peut se découper en plusieurs phases. A chacune d'elles il est possible d'associer une unité fonctionnelle. Considérons, pour illustrer notre propos, un microprocesseur disposant de trois unités :
- unité de recherche (R);
- unité de décodage (D);
- unité d'exécution (E).
dont on suppose qu'elles remplissent leurs fonctions respectives en un cycle d'horloge.
La figure 22 schématise de déroulement d'une instruction. La phase "recherche" mobilise l'unité de recherche pendant un cycle d'horloge. La phase "décodage" occupe l'unité de décodage pendant un deuxième cycle et la phase "exécution" utilise l'unité d'exécution pendant un troisième cycle. Il faut donc trois cycles d'horloge pour traiter une instruction. La prise en compte de l'instruction suivante se fait à partir du 4ème
cycle, et ainsi de suite. L'exécution de N instructions requiert donc 3 N cycles d'horloge (fig. 23).
Cependant nous constatons alors qu'à chaque cycle d'horloge deux des trois unités fonctionnelles sont inemployées. Il y a moyen d'accélérer les calculs en demandant à l'unité de recherche d'aller chercher l'instruction suivante dès le deuxième cycle d'horloge. Cette instruction est ensuite décodée au cycle suivant, alors que l'unité de recherche continue également. Nous obtenons alors le diagramme schématisé sur la figure 24. Un processeur dans lequel ce traitement anticipé est possible est dit avec pipeline. Le compteur ordinal est incrémenté à chaque cycle d'horloge.
Dans un processeur avec pipeline il faut toujours 3 cycles pour exécuter chaque instruction, mais dès qu'une instruction est terminée il suffit d'attendre un cycle pour que la suivante soit terminée, et non trois comme dans le cas précédent. Dans ces conditions il ne faut que N+2 cycles d'horloge pour exécuter N instructions. On calcule presque 3 fois plus vite.
Il n'est cependant pas simple de bénéficier de ce gain de performance en totalité. Les performances d’un pipeline peuvent être dégradées par des aléas. On distingue trois types d’aléas :
- aléas structurels : deux instructions ont besoin simultanément d’une même ressource ou d’un même bloc fonctionnel ;
- aléas de données : une instruction a besoin du résultat d’une instruction qui n’est pas terminée ;
- aléas de contrôle : rupture de séquence.
Par exemple lors d'une rupture de séquence (branchement conditionnel ou non, fin de boucle, appel de sous-programme, etc.), il faut gérer les instructions dont le traitement a été anticipé. Il existe généralement deux types de branchements : simple ou retardé. Pour un branchement simple le traitement anticipé est interrompu et la chaîne est vidée avant d'exécuter le branchement. Il faut ensuite attendre à nouveau trois cycles pour obtenir un résultat. Pour un branchement retardé on termine le traitement commencé avant d'exécuter le branchement. Une bonne utilisation de ces branchements permet d'optimiser le fonctionnement du processeur. On peut trouver dans certains processeurs une unité qui cherche à anticiper la destination d'un branchement on parle de prédiction de la destination. Souvent l’adresse du branchement estcontenue dans l’instruction de branchement, il est alors possible de charger l’instruction suivante dans le pipeline. C’est moins facile pour l’adresse de retour d’une fonction qui est stockée dans la pile. La prédiction de condition est plus difficile à réaliser. On procède de manière statistique par exemple. Ainsi en fin de boucle on revient systématiquement au début, sauf la dernière fois.
Le traitement des interruptions, que nous étudierons dans le prochain chapitre, pose également quelques problèmes. En général, pour simplifier la gestion de la reprise du programme interrompu, les instructions engagées dans le pipeline sont traitées avant la prise en compte effective de l'interruption. Selon la longueur du pipeline cela peut générer un retard significatif.
Selon leur complexité, la durée de traitement de toutes les instructions n'est pas nécessairement identique. C'est particulièrement vrai en cas d'accès à la mémoire. Pour que les difficultés soient plus visibles considérons un processeur avec une quatrième unité fonctionnelle chargée de l'éventuelle lecture en mémoire des opérandes :
- unité de recherche (R);
- unité de décodage (D);
- unité de lecture (L);
- unité d'exécution (E).
Comme l'unité de lecture n'est pas toujours sollicitée le traitement d'une instruction prend 3 ou 4 cycles. Considérons le traitement de deux instructions consécutives I1 et I2, la première écrivant en mémoire, la seconde lisant en mémoire. La figure 25 illustre un conflit dans le traitement de ces deux accès. L'unité de lecture pour le besoin de l'instruction I2 aurait dû fonctionner au 4ème cycle d'horloge. Mais simultanément l'unité d'exécution aurait été en train d'écrire en mémoire. Le traitement de l'instruction I2 est donc pénalisé d'un cycle.
Il peut également y avoir conflit entre une instruction effectuant un accès mémoire et la recherche de l’instruction suivante. La séparation des instructions et des données permet de remédier à ce type d’aléas.
Nous avons simplifié. Le temps d'accès à la mémoire peut correspondre à plusieurs cycles d'horloge. D'autre part ce temps d'accès peut être variable. Ainsi deux instructions consécutives peuvent faire appel au même bloc mémoire ou à deux blocs différents. En fonction de l'architecture de la mémoire nous savons que les temps d'accès pour les deux instructions peuvent être identiques dans un cas et différents dans l'autre.
Par ailleurs, il peut y avoir dépendance entre deux instructions, la seconde ayant besoin d'une adresse calculée par la première par exemple.
La gestion de ces problèmes est généralement résolue par les compilateurs qui peuvent insérer des instructions NOP ou permuter des instructions du programme en tenant compte des spécificités du processeur.
12 - Unités d'exécution parallèles
Dans le précédent paragraphe nous avons étudié le découpage principalement de l'unité de commande en unités fonctionnelles pouvant travailler en parallèle. On peut également trouver plusieurs unités d'exécution ou de calcul.
L'unité de commande choisit l'unité à utiliser en fonction du type de l'instruction : ALU, FPU (Floating Point Unit) ou unité multimédia. Ce mode de fonctionnement ressemble à l'utilisation d'un coprocesseur. Un coprocesseur n'est pas utilisé pour exécuter du traitement parallèle mais pour augmenter ou améliorer les fonctionnalités du CPU. Celui-ci charge des registres pour fournir des données au coprocesseur, démarre ce dernier et se suspend jusqu'à ce que le traitement demandé soit effectué. En fin d'exécution le coprocesseur place le résultat dans un registre, réveille le processeur principal et se suspend jusqu'à une nouvelle requête. Un coprocesseur peut permettre d'augmenter l'ensemble des instructions ou réaliser certains calculs plus rapidement que l'unité centrale ("coprocesseur flottant").
Si le processeur est capable d'exécuter en parallèle plusieurs instructions différentes sur plusieurs unités d'exécution il est dit superscalaire. Il peut en particulier disposer de plusieurs unités arithmétiques et logiques parallèles. L’unité de commande dispose d’un bloc de distribution qui détermine au fur et à mesure quelles instructions peuvent être traitées en parallèle. Il faut également être capable de faire passer rapidement les résultats intermédiaires d’une unité d’exécution à une autre. Les performances d'une machine superscalaire peuvent être améliorées si le compilateur est capable d'identifier les instructions pouvant être exécutées simultanément, c'est-à-dire sans dépendance. L'approche Très Long Mot Instruction (VLIW : Very Long Instruction Word) est assez similaire, mais le parallélisme est totalement géré par le compilateur. Les instructions pouvant être exécutées simultanément sont placées dans un mot de grande longueur (128 bits pour i860 d'Intel).
On peut également imaginer un processeur avec une unité de contrôle mais disposant de n unités d'exécution identiques et de n ensembles de registres. Cet ordinateur peut donc exécuter simultanément le même calcul sur n jeux de données. Cette configuration est appelée SIMD (Single Instruction on Multiple Data) ou processeur vectoriel.
13 - Processus RISC
En première approximation la puissance d'un système peut être identifiée au temps d'exécution d'une tâche. Celui-ci peut s'écrire sous la forme suivante :
temps/tâche = Nb.instructions/tâche x Nb.cycles/instruction x temps/cycle
Le nombre de cycles par instruction est une moyenne, mais il doit tenir compte des transferts entre la mémoire et le processeur, y compris celui de l'instruction elle-même. Pour améliorer les performances, on peut donc agir sur chacun de ces trois termes, en tenant compte de leurs corrélations.
Le dernier terme correspond évidemment à la fréquence de l'horloge. L'évolution, dans un premier temps, a consisté à chercher la diminution du nombre d'instructions dans un programme, en utilisant des instructions et des modes d'adressage de plus en plus sophistiqués. Puis est apparue une philosophie différente qui cherche à réduire le nombre de cycles nécessaires à la réalisation de chaque instruction. Cette approche s'est appuyée sur les progrès réalisés en matière de matériel (mémoire virtuelle, cache, unité de gestion de mémoire, pipeline, etc.) et logiciel (compilateurs).
Le concept RISC (Reduced Instruction Set Computer) est apparu en 1975 chez IBM (IBM801 de John Coke), d'après des idées de Seymour Cray, avant d'être approfondi dans les années 80 par les universités de Stanford et Berkeley. Il repose sur la constatation que même les systèmes ou les applications les plus sophistiqués n'utilisent qu'une petite fraction du jeu d'instructions à leur disposition.
Des études statistiques, portant sur un grand nombre de systèmes d'exploitation et d'applications réels, ont montré que :
- Dans 80 % d'un programme on n'utilise que 20 % du jeu d'instructions.
- Les opérations les plus usitées sont :
· les opérations d'échange entre l'unité centrale et la mémoire;
· les appels à des sous-programmes.
- L'instruction d'appel d'une procédure est la plus gourmande en temps : sauvegarde et restitution du contexte et passage des paramètres.
- 80 % des variables locales sont des scalaires.
- 90 % des structures de données complexes sont des variables globales.
- La profondeur maximale d'appels imbriqués est en moyenne de huit. Une profondeur plus importante ne se rencontre que dans 1 % des cas.
Les processeurs classiques sont désormais appelés CISC (Complex Instruction Set Computer) par opposition au terme RISC.
L'apparition de mémoires très rapides à un coût très faible a constitué un des principaux arguments technologiques ayant favorisé les processeurs RISC. A l'origine les temps de décodage d'une instruction complexe et d'exécution du microcode correspondant étaient masqués par les temps d'accès à la mémoire. En réduisant celui-ci, le goulot d'étranglement s'est déplacé vers les unités de décodage et d'exécution. Il a donc fallu envisager un jeu d'instructions élémentaires câblées simplifiant l'architecture du processeur et réduisant les temps d'exécution. D'autre part, la capacité mémoire n'étant pratiquement plus limitée il n'y avait pas d'obstacle à augmenter la taille des programmes : la fonctionnalité de chaque instruction étant limitée il faut générer un plus grand nombre d'instructions (en pratique pas plus de 30 %).
Par contre la génération de code est plus compliquée. Les instructions complexes facilitent la traduction des programmes écrits en langage évolué. C'est également au compilateur de se charger de l'optimisation du code en fonction des caractéristiques des processeurs. Les recherches ayant débouché sur les processeurs RISC ont également porté sur les compilateurs. L'évolution des outils logiciels a vu l'émergence de compilateurs évolués permettant une optimisation efficace des codes générés avec des gains de l'ordre de 20 % en temps d'exécution. Le développement des compilateurs, pris en charge par les concepteurs de systèmes, et le développement des architectures sont très interdépendants.
Passons en revue les idées de base qui font la spécificité des architectures RISC. L'objectif recherché est d'exécuter une instruction à chaque cycle d'horloge. Ceci est rarement réalisé sur la totalité du jeu d'instructions. L'obtention de cette performance repose sur la mise en œuvre de plusieurs principes :
- simplification des instructions;
- simplification du format : longueur fixe des instructions et des champs;
- restriction des modes d'adressage;
- séquenceur câblé pour une exécution rapide;
- utilisation intensive de registres très nombreux;
- limitation des accès mémoire à deux instructions : LOAD et STORE;
- utilisation de caches;
- traitement anticipé des instructions (pipeline) : ce qui permet d'obtenir un résultat à chaque cycle.
Le rôle du compilateur est essentiel pour l'optimisation du code engendré. Un effort particulier est fait sur les points suivants :
- allocation optimale des registres;
- élimination des redondances;
- optimisation des boucles, en ne conservant à l'intérieur que ce qui est modifié;
- optimisation du pipeline;
- optimisation du choix des instructions.
Le compilateur doit être capable d'exploiter au maximum les caractéristiques de l'architecture.
La figure 26 illustre l'influence du temps d'accès de la mémoire sur les performances de deux processeurs (RISC et CISC) cadencés à 20 MHz. La performance maximale de l'architecture RISC sert de référence (performance relative = 1). On observe une nette différence de comportement entre ces deux courbes. Pour un temps d'accès mémoire inférieur ou égal à un cycle d'horloge (50 ns) il n'y a pas amélioration des performances pour l'architecture CISC qui sature. Par contre dans les mêmes conditions on constate un gain important (ici un facteur 2) en performance pour le processeur RISC. Par contre celui-ci n'est compétitif que lorsqu'il est associé à une mémoire rapide. Cette figure explique le développement presque exclusif des architectures CISC jusqu'à l'apparition d'une nouvelle génération de mémoires rapides.
La simplicité des processeurs RISC fournit au moins deux autres avantages : le coût du développement et la surface de silicium sont notablement réduits. Plus simple un processeur RISC nécessite moins de temps et moins de main d'œuvre pour sa conception et sa mise au point. Par exemple le prototype RISC-II de l'université de Berkeley a été développé en deux ans par deux étudiants. De même le processeur ARM a été élaboré en dix-huit mois par une équipe de quatre personnes (6 hommes-ans). Par contre le 80386 d'Intel a demandé 100 hommes-ans. Le risque d'erreur de conception pouvant avoir un impact sur la clientèle avec retour de composants par exemple est aussi beaucoup plus faible. Le rapport coût/performance est donc largement en faveur des processeurs RISC. Par contre le développement des compilateurs est beaucoup plus
long. Dans un processeur CISC l'unité de contrôle occupe plus de 50 % de la surface de la plaquette silicium. Dans un processeur RISC elle en occupe moins de 20 %, il reste donc plus de place pour intégrer registres, caches, unités d'exécution parallèles et unités de gestion.
Il nous reste à décrire une organisation particulière des registres internes que l'on rencontre dans certaines architectures RISC. Elle est identifiée sous la dénomination de technique des fenêtres de registres. destinée à faciliter le passage de paramètres lors d'appel de procédures. Le nombre des registres est toujours important dans un processeur RISC. Il y avait par exemple 138 registres dans le prototype RISC-I de Berkeley avec lequel la technique a été développée. Celle-ci repose sur les statistiques déjà mentionnées sur le partage des variables et la profondeur d'imbrication des appels de procédures. Pour le RISC-I les dix premiers registres, accessibles à tous les niveaux, sont destinés à recevoir les variables globales. Les 128 registres suivants sont divisés en huit groupes ou fenêtres. Chaque groupe correspond à une profondeur d'appel. La profondeur maximale est donc limitée à huit. Les six premiers registres d'un bloc servent à l'échange des informations avec l'étage supérieur. Les dix autres sont disponibles pour les variables locales. Outre les registres globaux, chaque niveau intermédiaire dispose donc de vingt-deux registres : les seize qui lui sont propres et les six premiers registres de l'étage suivant (fig. 27). Cette technique simplifie les échanges d'informations entre les procédures appelantes et appelées. Elle demande cependant beaucoup de temps lors de la sauvegarde des registres en cas d'interruption.
Les architectures CISC et RISC, utilisant les mêmes technologies, ont de plus en plus tendance a se rapprocher. Certains processeurs, par exemple, traduisent les instructions CISC en suites d'instructions RISC avant l'exécution. Cela permet d'assurer la compatibilité des nouveaux processeurs avec tous les logiciels développés antérieurement, ce qui est indispensable si on veut pouvoir vendre le nouveau processeur.
14 - Evaluation des performances
Il est très important, pour le concepteur comme pour le client, de pouvoir évaluer les performances d'une machine. Pour cela l'idéal serait de pouvoir faire appel à un programme de test (benchmark) synthétisant l'ensemble des performances d'une architecture. Un tel programme universel n'existe pas. Par contre il existe un grand nombre de programmes de tests. Chacun de ces tests permet d'évaluer certains types de caractéristiques. Les tests peuvent être classés en trois familles :
- Les tests élaborés par les concepteurs de systèmes.
- Les tests adaptés à des applications spécifiques : par exemple le CERN compare les performances des machines en utilisant des programmes représentatifs des applications habituelles en physique des particules : analyses de données et simulations. C'est très certainement la meilleure solution.
- Les tests publics.
Parmi ces derniers nous pouvons citer : Dhrystone, Linpack, Whestone, Doduc, etc. Par exemple Dhrystone est destiné à mesurer l'efficacité des processeurs et compilateurs pour des programmes écrits en langage C. Pour cette raison il fait souvent référence dans le monde UNIX. Il est basé sur une étude statistique des instructions relevées dans un millier de programmes réels. Il ne fait pas intervenir les opérations en virgule flottante, les opérations d'entrées/sorties et les appels aux fonctions systèmes. Le test consiste à exécuter une boucle de programme un nombre fixe de fois. La performance est exprimée en Dhrystone/seconde : le nombre moyen de boucles exécutées par seconde. Le test de Linpack, écrit en FORTRAN, est surtout destiné au domaine scientifique et en particulier aux calculateurs vectoriels. Il est basé sur le temps nécessaire à la résolution d'un système linéaire de 100 (300 ou même 1000) équations à 100 (300 ou 1000) inconnues. Les résultats sont exprimés en Mflops : millions d'opérations flottantes par seconde. On parle maintenant en Gflops et Tflops. Whestone est destiné à l'évaluation des performances arithmétiques et en particulier celles des co-processeurs.
L'unité la plus fréquemment rencontrée dans la littérature publicitaire est le MIPS : million d'instructions par seconde. Il faut cependant être très prudent. Par exemple les fonctionnalités des instructions sont loin d'être comparables d'une machine à l'autre : plusieurs instructions pour un processeur peuvent être nécessaires pour obtenir le même résultat qu'une instruction d'un jeu plus complexe. D'autre part, lorsque le temps d'exécution n'est pas le même pour toutes les instructions il est indispensable de savoir quels types d'instructions ont été utilisés pour effectuer l'évaluation.
D'autre part pour que les comparaisons puissent être significatives il faut assurer une standardisation des programmes d'évaluation. C'est le but par exemple d'une commission regroupant quatorze constructeurs créée en 1988 : la SPEC (System Performance Evaluation Cooperative). La SPEC a initialement retenu 10 programmes principalement écrits en C et en FORTRAN. Le temps d'exécution de chacun de ces programmes est comparé à un temps de référence : le temps d'exécution sur Vax 11/780. Le rapport entre cette référence et le temps d'exécution sur le système testé constitue un SPECratio. La moyenne pour les dix programmes fournit la mesure finale exprimée en SPECmark. Depuis 1992 on distingue performances pour les calculs en entiers ou en flottants : SPECInt92 et SEPECfp92.
Un champ adresse peut permettre de référencer un registre ou un mot en mémoire. Il peut contenir le numéro du registre ou l'adresse effective du mot mais ce ne sont pas les seules manières d'identifier un opérande. Pour faciliter la programmation il existe de nombreux modes d'adressage. Le mode est défini soit par le code opération lorsque celui-ci impose un type déterminé, soit par un code faisant partie du champ adresse.
Les exemples ci-dessous sont empruntés aux instructions de l'assembleur PDP-11.
Adressage implicite : Le code opération identifie automatiquement l'opérande, l'instruction ne peut porter que sur un registre particulier. Par exemple, le test sur le signe du résultat d'une opération arithmétique concerne le registre d'état RE. Dans certaines architectures les transferts avec la mémoire ne se font qu’à partir ou à destination du registre d’accumulation. Dans ces cas aucun champ adresse n'est nécessaire.
Adressage immédiat : La valeur de l'opérande est contenue dans le champ adresse si le nombre de bits dans ce champ est suffisant, sinon dans le mot suivant l'instruction.
MOV #100, R1
Après cette instruction le registre R1 contient la valeur 100.
Adressage registre : Le champ adresse contient le numéro du registre opérande.
CLR R3
Après cette instruction le contenu de R3 est nul.
Adressage direct : Le champ adresse de l'instruction (ou le mot suivant si le nombre de bits n'est pas suffisant) contient l'adresse effective de l'opérande.
100 : 250
MOV 100, R2
Après cette instruction le registre R2 contient le mot qui se situe à l'adresse 100 en mémoire, c'est-à-dire 250.
Adressage indirect : Le champ adresse (ou le mot suivant) contient l'adresse d'un pointeur : mot en mémoire qui contient l'adresse effective de l'opérande.
MOV (R1), R4
Après cette instruction R4 contient la valeur du mot dont l'adresse est contenue dans R1. Comme R1 vaut 100 on trouve 250 dans R4.
Adressage indexé : Ce mode d'adressage est très utile lorsqu'on travaille, par exemple, sur des tableaux. Considérons un bloc de n mots consécutifs débutant à l'adresse A. Le kième mot se
trouve à l'adresse A + (k − 1). Pour référencer ce mot il est possible d'utiliser un registre d'index. L'adresse effective est calculée en additionnant le contenu de ce registre d'index à l'adresse qui se trouve dans le champ adresse de l'instruction. Sur certaines machines tous les registres généraux peuvent être utilisés comme registres d'index. La présence d'un registre d'index s'accompagne généralement de la possibilité d'incrémentation et décrémentation automatiques.
MOV R4, 100(R3)+
CLR 100(R3)
Avant la première opération R3 est nul, donc le contenu de R4 est transféré à l'adresse 100. Après le registre R3 est incrémenté. L'instruction suivante permet de mettre à zéro le contenu du mot à
l'adresse suivante.
Adressage basé : L'adressage basé est comparable à l'adressage indexé mais cette fois l'adresse effective est obtenue en additionnant le contenu du registre de base au contenu du champ adresse de l'instruction. Ce mode d'adressage est utilisé par exemple en cas d'allocation dynamique de la mémoire : la position du programme en mémoire peut changer en fonction de la charge du système et il n'occupe pas toujours un espace contigu. Cette technique permet également de réduire le nombre de bits dans le champ adresse : le registre de base contient la première adresse d'un bloc de 2k mots et l'adresse (sur k bits) contenue dans l'instruction représente le déplacement à l'intérieur du bloc.
Adressage relatif : L'adresse effective est obtenue est additionnant le contenu du compteur ordinal au contenu du champ adresse de l'instruction. Ce type d'adressage est utilisé par exemple dans des instructions de branchement.
N'oublions pas que le calcul de l'adresse effective peut nécessiter quelques opérations (addition par exemple). L'utilisation de certains modes d'adressage sophistiqués (le 68020 de Motorola dispose par exemple d'une cinquantaine de modes d'adressage) peut donc augmenter le temps de traitement d'une instruction.
10 - Réalisation d’un multiplieur micro-programmé
Reprenons le multiplieur que nous avons étudié plus haut (§ VII.4). Il est basé sur une unité d’exécution et une unité de commande câblée. Nous voulons conserver l’unité d’exécution constituée de trois registres R0, R1 et ACC, un additionneur et un compteur. Le fonctionnement de cette unité est contrôlé par quatre signaux INIT, W_ACC, ITER et FIN, qui dépendent de deux signaux d’information R10 et C_max. Nous voulons remplacer l’automate de contrôle-commande par l’équivalent d’un séquenceur micro-programmé. Pour cela nous traduisons l’organigramme de la figure 6 en un micro-programme en pseudo-langage. L’exemple suivant se comprend aisément :
Nous n’avons ici que deux types d’instructions : des actions et un branchement conditionnel. Il suffit donc d’un bit pour identifier ce type, choisissons 0 pour les actions et 1 pour le branchement conditionnel.
Nous avons quatre actions (INIT, ADD, ITER et STOP) il nous faut donc deux bits pour les identifier. Ces instructions s’adressent implicitement à des éléments fonctionnels, nous n’avons donc pas besoin de champ supplémentaire.
Pour un branchement conditionnel il faut identifier la condition et l’adresse de saut. Il y a deux tests différents un bit est donc suffisant. Le micro-programme compte six instructions, il faut donc trois bits d’adresse. La longueur minimale d’une micro-instruction est donc cinq bit. Nous choisissons le format suivant, qui dépend du bit le plus significatif (bit 4) indiquant le type d’instruction.
Action :
- bit 4 : 0
- bits 3 et 2 : 00 INIT
01 ADD
10 ITER
11 STOP
- bits 0 et 1 : 00 (inutilisés)
Branchement conditionnel :
- bit 4 : 1
- bit 3 : 0 test sur R10
101 test sur C_max
- bits 0 à 2 : adresse de saut
Nous pouvons traduire le micro-programme en binaire en utilisant cette convention :
Nous devons concevoir le circuit de commande destiné à exploiter ce micro-programme. Nous avons besoin d’une mémoire d’au moins 6 mots de 5 bits, d’un compteur pour adresser cette mémoire et d’un registre de 5 bits pour contenir la micro-instruction courante.
Il nous faut un transcodeur pour produire les signaux de commande à partir des deux bits du champ action. Pour cela il est possible d’utiliser un démultiplexeur (fig. 21).
Lors d’un test positif le compteur doit être chargé à partir du champ adresse. La commande de chargement parallèle correspond donc à l’expression logique suivante :
Chrgt //= Op Condition
où Op représente le type d’instruction (bit 4 du registre micro-instruction) et Condition le signal indiquant si la condition du test est réalisée :
µr3 est le bit 3 du registre micro-instruction. Dans les autres cas le compteur doit être incrémenter d’une unité. Le comptage doit être bloqué lorsque la multiplication est terminée, pour cela nous pouvons employer le signal fin. Ce qui nous donne :
Le signal extérieur Start de démarrage de la multiplication, si l’opération précédente est terminée, doit faire une remise à zéro du compteur pour relancer le micro-programme à l’instruction INIT. Nous avons simplifié la lecture de la mémoire micro-programme en supposant que l’affichage de l’adresse suffisait à transférer la micro-instruction courante dans le registre.
11 - Traitement anticipé des instructions : pipeline
Nous avons vu que le traitement d'une instruction peut se découper en plusieurs phases. A chacune d'elles il est possible d'associer une unité fonctionnelle. Considérons, pour illustrer notre propos, un microprocesseur disposant de trois unités :
- unité de recherche (R);
- unité de décodage (D);
- unité d'exécution (E).
dont on suppose qu'elles remplissent leurs fonctions respectives en un cycle d'horloge.
La figure 22 schématise de déroulement d'une instruction. La phase "recherche" mobilise l'unité de recherche pendant un cycle d'horloge. La phase "décodage" occupe l'unité de décodage pendant un deuxième cycle et la phase "exécution" utilise l'unité d'exécution pendant un troisième cycle. Il faut donc trois cycles d'horloge pour traiter une instruction. La prise en compte de l'instruction suivante se fait à partir du 4ème
cycle, et ainsi de suite. L'exécution de N instructions requiert donc 3 N cycles d'horloge (fig. 23).
Cependant nous constatons alors qu'à chaque cycle d'horloge deux des trois unités fonctionnelles sont inemployées. Il y a moyen d'accélérer les calculs en demandant à l'unité de recherche d'aller chercher l'instruction suivante dès le deuxième cycle d'horloge. Cette instruction est ensuite décodée au cycle suivant, alors que l'unité de recherche continue également. Nous obtenons alors le diagramme schématisé sur la figure 24. Un processeur dans lequel ce traitement anticipé est possible est dit avec pipeline. Le compteur ordinal est incrémenté à chaque cycle d'horloge.
Dans un processeur avec pipeline il faut toujours 3 cycles pour exécuter chaque instruction, mais dès qu'une instruction est terminée il suffit d'attendre un cycle pour que la suivante soit terminée, et non trois comme dans le cas précédent. Dans ces conditions il ne faut que N+2 cycles d'horloge pour exécuter N instructions. On calcule presque 3 fois plus vite.
Il n'est cependant pas simple de bénéficier de ce gain de performance en totalité. Les performances d’un pipeline peuvent être dégradées par des aléas. On distingue trois types d’aléas :
- aléas structurels : deux instructions ont besoin simultanément d’une même ressource ou d’un même bloc fonctionnel ;
- aléas de données : une instruction a besoin du résultat d’une instruction qui n’est pas terminée ;
- aléas de contrôle : rupture de séquence.
Par exemple lors d'une rupture de séquence (branchement conditionnel ou non, fin de boucle, appel de sous-programme, etc.), il faut gérer les instructions dont le traitement a été anticipé. Il existe généralement deux types de branchements : simple ou retardé. Pour un branchement simple le traitement anticipé est interrompu et la chaîne est vidée avant d'exécuter le branchement. Il faut ensuite attendre à nouveau trois cycles pour obtenir un résultat. Pour un branchement retardé on termine le traitement commencé avant d'exécuter le branchement. Une bonne utilisation de ces branchements permet d'optimiser le fonctionnement du processeur. On peut trouver dans certains processeurs une unité qui cherche à anticiper la destination d'un branchement on parle de prédiction de la destination. Souvent l’adresse du branchement estcontenue dans l’instruction de branchement, il est alors possible de charger l’instruction suivante dans le pipeline. C’est moins facile pour l’adresse de retour d’une fonction qui est stockée dans la pile. La prédiction de condition est plus difficile à réaliser. On procède de manière statistique par exemple. Ainsi en fin de boucle on revient systématiquement au début, sauf la dernière fois.
Le traitement des interruptions, que nous étudierons dans le prochain chapitre, pose également quelques problèmes. En général, pour simplifier la gestion de la reprise du programme interrompu, les instructions engagées dans le pipeline sont traitées avant la prise en compte effective de l'interruption. Selon la longueur du pipeline cela peut générer un retard significatif.
Selon leur complexité, la durée de traitement de toutes les instructions n'est pas nécessairement identique. C'est particulièrement vrai en cas d'accès à la mémoire. Pour que les difficultés soient plus visibles considérons un processeur avec une quatrième unité fonctionnelle chargée de l'éventuelle lecture en mémoire des opérandes :
- unité de recherche (R);
- unité de décodage (D);
- unité de lecture (L);
- unité d'exécution (E).
Comme l'unité de lecture n'est pas toujours sollicitée le traitement d'une instruction prend 3 ou 4 cycles. Considérons le traitement de deux instructions consécutives I1 et I2, la première écrivant en mémoire, la seconde lisant en mémoire. La figure 25 illustre un conflit dans le traitement de ces deux accès. L'unité de lecture pour le besoin de l'instruction I2 aurait dû fonctionner au 4ème cycle d'horloge. Mais simultanément l'unité d'exécution aurait été en train d'écrire en mémoire. Le traitement de l'instruction I2 est donc pénalisé d'un cycle.
Il peut également y avoir conflit entre une instruction effectuant un accès mémoire et la recherche de l’instruction suivante. La séparation des instructions et des données permet de remédier à ce type d’aléas.
Nous avons simplifié. Le temps d'accès à la mémoire peut correspondre à plusieurs cycles d'horloge. D'autre part ce temps d'accès peut être variable. Ainsi deux instructions consécutives peuvent faire appel au même bloc mémoire ou à deux blocs différents. En fonction de l'architecture de la mémoire nous savons que les temps d'accès pour les deux instructions peuvent être identiques dans un cas et différents dans l'autre.
Par ailleurs, il peut y avoir dépendance entre deux instructions, la seconde ayant besoin d'une adresse calculée par la première par exemple.
La gestion de ces problèmes est généralement résolue par les compilateurs qui peuvent insérer des instructions NOP ou permuter des instructions du programme en tenant compte des spécificités du processeur.
12 - Unités d'exécution parallèles
Dans le précédent paragraphe nous avons étudié le découpage principalement de l'unité de commande en unités fonctionnelles pouvant travailler en parallèle. On peut également trouver plusieurs unités d'exécution ou de calcul.
L'unité de commande choisit l'unité à utiliser en fonction du type de l'instruction : ALU, FPU (Floating Point Unit) ou unité multimédia. Ce mode de fonctionnement ressemble à l'utilisation d'un coprocesseur. Un coprocesseur n'est pas utilisé pour exécuter du traitement parallèle mais pour augmenter ou améliorer les fonctionnalités du CPU. Celui-ci charge des registres pour fournir des données au coprocesseur, démarre ce dernier et se suspend jusqu'à ce que le traitement demandé soit effectué. En fin d'exécution le coprocesseur place le résultat dans un registre, réveille le processeur principal et se suspend jusqu'à une nouvelle requête. Un coprocesseur peut permettre d'augmenter l'ensemble des instructions ou réaliser certains calculs plus rapidement que l'unité centrale ("coprocesseur flottant").
Si le processeur est capable d'exécuter en parallèle plusieurs instructions différentes sur plusieurs unités d'exécution il est dit superscalaire. Il peut en particulier disposer de plusieurs unités arithmétiques et logiques parallèles. L’unité de commande dispose d’un bloc de distribution qui détermine au fur et à mesure quelles instructions peuvent être traitées en parallèle. Il faut également être capable de faire passer rapidement les résultats intermédiaires d’une unité d’exécution à une autre. Les performances d'une machine superscalaire peuvent être améliorées si le compilateur est capable d'identifier les instructions pouvant être exécutées simultanément, c'est-à-dire sans dépendance. L'approche Très Long Mot Instruction (VLIW : Very Long Instruction Word) est assez similaire, mais le parallélisme est totalement géré par le compilateur. Les instructions pouvant être exécutées simultanément sont placées dans un mot de grande longueur (128 bits pour i860 d'Intel).
On peut également imaginer un processeur avec une unité de contrôle mais disposant de n unités d'exécution identiques et de n ensembles de registres. Cet ordinateur peut donc exécuter simultanément le même calcul sur n jeux de données. Cette configuration est appelée SIMD (Single Instruction on Multiple Data) ou processeur vectoriel.
13 - Processus RISC
En première approximation la puissance d'un système peut être identifiée au temps d'exécution d'une tâche. Celui-ci peut s'écrire sous la forme suivante :
temps/tâche = Nb.instructions/tâche x Nb.cycles/instruction x temps/cycle
Le nombre de cycles par instruction est une moyenne, mais il doit tenir compte des transferts entre la mémoire et le processeur, y compris celui de l'instruction elle-même. Pour améliorer les performances, on peut donc agir sur chacun de ces trois termes, en tenant compte de leurs corrélations.
Le dernier terme correspond évidemment à la fréquence de l'horloge. L'évolution, dans un premier temps, a consisté à chercher la diminution du nombre d'instructions dans un programme, en utilisant des instructions et des modes d'adressage de plus en plus sophistiqués. Puis est apparue une philosophie différente qui cherche à réduire le nombre de cycles nécessaires à la réalisation de chaque instruction. Cette approche s'est appuyée sur les progrès réalisés en matière de matériel (mémoire virtuelle, cache, unité de gestion de mémoire, pipeline, etc.) et logiciel (compilateurs).
Le concept RISC (Reduced Instruction Set Computer) est apparu en 1975 chez IBM (IBM801 de John Coke), d'après des idées de Seymour Cray, avant d'être approfondi dans les années 80 par les universités de Stanford et Berkeley. Il repose sur la constatation que même les systèmes ou les applications les plus sophistiqués n'utilisent qu'une petite fraction du jeu d'instructions à leur disposition.
Des études statistiques, portant sur un grand nombre de systèmes d'exploitation et d'applications réels, ont montré que :
- Dans 80 % d'un programme on n'utilise que 20 % du jeu d'instructions.
- Les opérations les plus usitées sont :
· les opérations d'échange entre l'unité centrale et la mémoire;
· les appels à des sous-programmes.
- L'instruction d'appel d'une procédure est la plus gourmande en temps : sauvegarde et restitution du contexte et passage des paramètres.
- 80 % des variables locales sont des scalaires.
- 90 % des structures de données complexes sont des variables globales.
- La profondeur maximale d'appels imbriqués est en moyenne de huit. Une profondeur plus importante ne se rencontre que dans 1 % des cas.
Les processeurs classiques sont désormais appelés CISC (Complex Instruction Set Computer) par opposition au terme RISC.
L'apparition de mémoires très rapides à un coût très faible a constitué un des principaux arguments technologiques ayant favorisé les processeurs RISC. A l'origine les temps de décodage d'une instruction complexe et d'exécution du microcode correspondant étaient masqués par les temps d'accès à la mémoire. En réduisant celui-ci, le goulot d'étranglement s'est déplacé vers les unités de décodage et d'exécution. Il a donc fallu envisager un jeu d'instructions élémentaires câblées simplifiant l'architecture du processeur et réduisant les temps d'exécution. D'autre part, la capacité mémoire n'étant pratiquement plus limitée il n'y avait pas d'obstacle à augmenter la taille des programmes : la fonctionnalité de chaque instruction étant limitée il faut générer un plus grand nombre d'instructions (en pratique pas plus de 30 %).
Par contre la génération de code est plus compliquée. Les instructions complexes facilitent la traduction des programmes écrits en langage évolué. C'est également au compilateur de se charger de l'optimisation du code en fonction des caractéristiques des processeurs. Les recherches ayant débouché sur les processeurs RISC ont également porté sur les compilateurs. L'évolution des outils logiciels a vu l'émergence de compilateurs évolués permettant une optimisation efficace des codes générés avec des gains de l'ordre de 20 % en temps d'exécution. Le développement des compilateurs, pris en charge par les concepteurs de systèmes, et le développement des architectures sont très interdépendants.
Passons en revue les idées de base qui font la spécificité des architectures RISC. L'objectif recherché est d'exécuter une instruction à chaque cycle d'horloge. Ceci est rarement réalisé sur la totalité du jeu d'instructions. L'obtention de cette performance repose sur la mise en œuvre de plusieurs principes :
- simplification des instructions;
- simplification du format : longueur fixe des instructions et des champs;
- restriction des modes d'adressage;
- séquenceur câblé pour une exécution rapide;
- utilisation intensive de registres très nombreux;
- limitation des accès mémoire à deux instructions : LOAD et STORE;
- utilisation de caches;
- traitement anticipé des instructions (pipeline) : ce qui permet d'obtenir un résultat à chaque cycle.
Le rôle du compilateur est essentiel pour l'optimisation du code engendré. Un effort particulier est fait sur les points suivants :
- allocation optimale des registres;
- élimination des redondances;
- optimisation des boucles, en ne conservant à l'intérieur que ce qui est modifié;
- optimisation du pipeline;
- optimisation du choix des instructions.
Le compilateur doit être capable d'exploiter au maximum les caractéristiques de l'architecture.
La figure 26 illustre l'influence du temps d'accès de la mémoire sur les performances de deux processeurs (RISC et CISC) cadencés à 20 MHz. La performance maximale de l'architecture RISC sert de référence (performance relative = 1). On observe une nette différence de comportement entre ces deux courbes. Pour un temps d'accès mémoire inférieur ou égal à un cycle d'horloge (50 ns) il n'y a pas amélioration des performances pour l'architecture CISC qui sature. Par contre dans les mêmes conditions on constate un gain important (ici un facteur 2) en performance pour le processeur RISC. Par contre celui-ci n'est compétitif que lorsqu'il est associé à une mémoire rapide. Cette figure explique le développement presque exclusif des architectures CISC jusqu'à l'apparition d'une nouvelle génération de mémoires rapides.
La simplicité des processeurs RISC fournit au moins deux autres avantages : le coût du développement et la surface de silicium sont notablement réduits. Plus simple un processeur RISC nécessite moins de temps et moins de main d'œuvre pour sa conception et sa mise au point. Par exemple le prototype RISC-II de l'université de Berkeley a été développé en deux ans par deux étudiants. De même le processeur ARM a été élaboré en dix-huit mois par une équipe de quatre personnes (6 hommes-ans). Par contre le 80386 d'Intel a demandé 100 hommes-ans. Le risque d'erreur de conception pouvant avoir un impact sur la clientèle avec retour de composants par exemple est aussi beaucoup plus faible. Le rapport coût/performance est donc largement en faveur des processeurs RISC. Par contre le développement des compilateurs est beaucoup plus
long. Dans un processeur CISC l'unité de contrôle occupe plus de 50 % de la surface de la plaquette silicium. Dans un processeur RISC elle en occupe moins de 20 %, il reste donc plus de place pour intégrer registres, caches, unités d'exécution parallèles et unités de gestion.
Il nous reste à décrire une organisation particulière des registres internes que l'on rencontre dans certaines architectures RISC. Elle est identifiée sous la dénomination de technique des fenêtres de registres. destinée à faciliter le passage de paramètres lors d'appel de procédures. Le nombre des registres est toujours important dans un processeur RISC. Il y avait par exemple 138 registres dans le prototype RISC-I de Berkeley avec lequel la technique a été développée. Celle-ci repose sur les statistiques déjà mentionnées sur le partage des variables et la profondeur d'imbrication des appels de procédures. Pour le RISC-I les dix premiers registres, accessibles à tous les niveaux, sont destinés à recevoir les variables globales. Les 128 registres suivants sont divisés en huit groupes ou fenêtres. Chaque groupe correspond à une profondeur d'appel. La profondeur maximale est donc limitée à huit. Les six premiers registres d'un bloc servent à l'échange des informations avec l'étage supérieur. Les dix autres sont disponibles pour les variables locales. Outre les registres globaux, chaque niveau intermédiaire dispose donc de vingt-deux registres : les seize qui lui sont propres et les six premiers registres de l'étage suivant (fig. 27). Cette technique simplifie les échanges d'informations entre les procédures appelantes et appelées. Elle demande cependant beaucoup de temps lors de la sauvegarde des registres en cas d'interruption.
Les architectures CISC et RISC, utilisant les mêmes technologies, ont de plus en plus tendance a se rapprocher. Certains processeurs, par exemple, traduisent les instructions CISC en suites d'instructions RISC avant l'exécution. Cela permet d'assurer la compatibilité des nouveaux processeurs avec tous les logiciels développés antérieurement, ce qui est indispensable si on veut pouvoir vendre le nouveau processeur.
14 - Evaluation des performances
Il est très important, pour le concepteur comme pour le client, de pouvoir évaluer les performances d'une machine. Pour cela l'idéal serait de pouvoir faire appel à un programme de test (benchmark) synthétisant l'ensemble des performances d'une architecture. Un tel programme universel n'existe pas. Par contre il existe un grand nombre de programmes de tests. Chacun de ces tests permet d'évaluer certains types de caractéristiques. Les tests peuvent être classés en trois familles :
- Les tests élaborés par les concepteurs de systèmes.
- Les tests adaptés à des applications spécifiques : par exemple le CERN compare les performances des machines en utilisant des programmes représentatifs des applications habituelles en physique des particules : analyses de données et simulations. C'est très certainement la meilleure solution.
- Les tests publics.
Parmi ces derniers nous pouvons citer : Dhrystone, Linpack, Whestone, Doduc, etc. Par exemple Dhrystone est destiné à mesurer l'efficacité des processeurs et compilateurs pour des programmes écrits en langage C. Pour cette raison il fait souvent référence dans le monde UNIX. Il est basé sur une étude statistique des instructions relevées dans un millier de programmes réels. Il ne fait pas intervenir les opérations en virgule flottante, les opérations d'entrées/sorties et les appels aux fonctions systèmes. Le test consiste à exécuter une boucle de programme un nombre fixe de fois. La performance est exprimée en Dhrystone/seconde : le nombre moyen de boucles exécutées par seconde. Le test de Linpack, écrit en FORTRAN, est surtout destiné au domaine scientifique et en particulier aux calculateurs vectoriels. Il est basé sur le temps nécessaire à la résolution d'un système linéaire de 100 (300 ou même 1000) équations à 100 (300 ou 1000) inconnues. Les résultats sont exprimés en Mflops : millions d'opérations flottantes par seconde. On parle maintenant en Gflops et Tflops. Whestone est destiné à l'évaluation des performances arithmétiques et en particulier celles des co-processeurs.
L'unité la plus fréquemment rencontrée dans la littérature publicitaire est le MIPS : million d'instructions par seconde. Il faut cependant être très prudent. Par exemple les fonctionnalités des instructions sont loin d'être comparables d'une machine à l'autre : plusieurs instructions pour un processeur peuvent être nécessaires pour obtenir le même résultat qu'une instruction d'un jeu plus complexe. D'autre part, lorsque le temps d'exécution n'est pas le même pour toutes les instructions il est indispensable de savoir quels types d'instructions ont été utilisés pour effectuer l'évaluation.
D'autre part pour que les comparaisons puissent être significatives il faut assurer une standardisation des programmes d'évaluation. C'est le but par exemple d'une commission regroupant quatorze constructeurs créée en 1988 : la SPEC (System Performance Evaluation Cooperative). La SPEC a initialement retenu 10 programmes principalement écrits en C et en FORTRAN. Le temps d'exécution de chacun de ces programmes est comparé à un temps de référence : le temps d'exécution sur Vax 11/780. Le rapport entre cette référence et le temps d'exécution sur le système testé constitue un SPECratio. La moyenne pour les dix programmes fournit la mesure finale exprimée en SPECmark. Depuis 1992 on distingue performances pour les calculs en entiers ou en flottants : SPECInt92 et SEPECfp92.












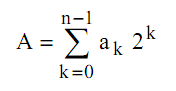









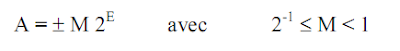








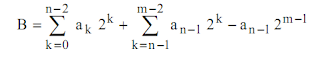
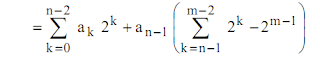




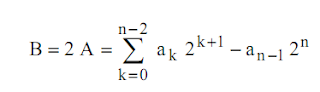



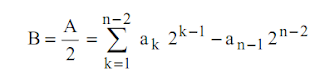



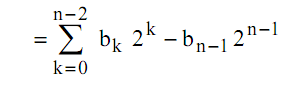










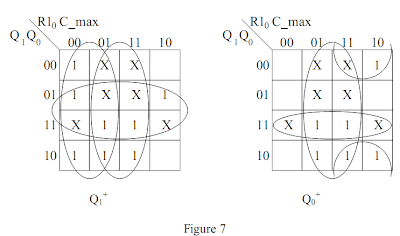





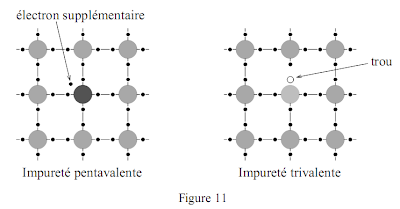










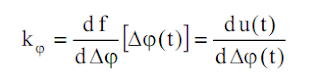










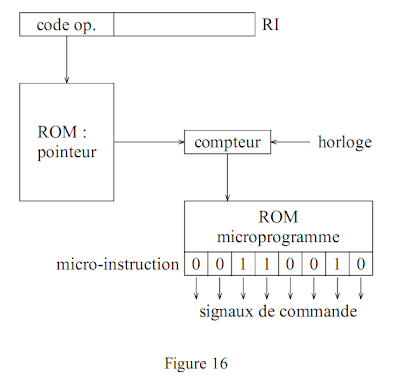
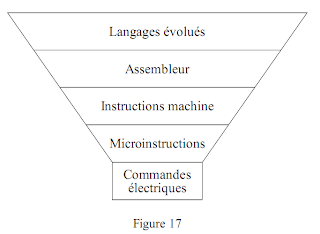













There are many informations
RépondreSupprimerThanks 👍😊