- Correction.
Exercice 1 – Algèbre de Boole
a) En utilisant exclusivement l’algèbre booléene, démontrez que :
On calcule les formes canoniques disjonctives des deux expressions :
De même,
Après distribution et commutation, on obtient les deux mêmes expressions.
b) Par Shannon, sur la variable A, il vient :
Par Shannon sur la variable B, il vient :
c) En utilisant une technique de votre choix, démontrez que le circuit suivant a toujours sa sortie fausse :
Soit X, la sortie du XNOR(B,C), il vient, par Shannon sur la variable X :
Exercice 2 – Analyse et synthèse de circuits
1) Trouver l’expression disjonctive simplifiée de X au moyen de la table de Karnaugh.
Évaluez son coût minimal et dessinez votre meilleur circuit
Dessinez le circuit ci-dessous
2) La fonction FY a déjà été réalisée par un apprenti. Elle fonctionne bien mais le patron prétend que le circuit coûte trop cher pour rien. Faites l’analyse de cette fonction et proposez votre meilleur circuit en comparant les versions disjonctive et conjonctive.
a) version disjonctive
b) version conjonctive
c) Votre patron vous demande de porter un regard critique sur la première implantation de FY. Qu’allez-vous lui dire ?
C’était une bonne idée d’utiliser la forme conjonctive. Toutefois, deux erreurs ont été commises :
1) 3 impliqués alors que 2 auraient suffi
2) L’utilisation de portes NOR aurait été moins couteuse
Conclusion, le patron avait raison, le circuit coute (2+2)+(3+2)+(3+2)+(3+2), soit 19 à la place de 9.
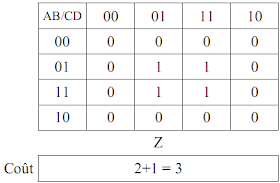
3) Sachant que finalement, seule la valeur de Z importe, proposez votre meilleur circuit pour implanter Z(A,B,C,D)
Dessinez le circuit optimisé.
Exercice 3 - Quine-McCluskey
1)
2) Procéder par la méthode Quine-McCluskey pour simplifier la fonction F(A,B,C,D) et identifier les impliquants premiers
3) Impliquants essentiels : 0X1X
4)

Soient 4 solutions optimales avec 3 impliquants premiers (+ l’impliquant essentiel)
5) Confirmez votre résultat en utilisant une table de Karnaugh
Exercice 4 - Décodeur
Exercice 5 - multiplexeur














thinks
RépondreSupprimer