Cours Normalisation les Quatres Formes Normales - Boyce-Codd(BCNF) et Dépendances Fonctionnelles bases de données

But de la normalisation

  

• Objectif : construire un schéma relationnel évitant la redondance

• La redondance implique des anomalies lors de :

• l'insertion (nouvel employé, nouveau département)

• la suppression (du dernier employé d'un département)

• la modification (changement de manager)

  

Dépendances fonctionnelles (DF)

DF1 : SSN --> [EName; BDate; Address;D#]

DF2 : D# --> [DName;DMgrSSN]

Il y a une dépendance fonctionnelle X --> Y (X détermine Y)

si pour chaque paire de tuple t₁; t₂ de R,

 

si t₁[X]= t₂[X] alors t₁[Y ]= t₂[Y ].

 

 

Dépendances fonctionnelles : exemple 

       

DF1 : SSN -->[EName; BDate; Address;D#]
     DF2 : D# --> [DName;DMgrSSN]

EmpDept

  

Première forme normale

Une relation R est en première forme normale si :  
  

• R respecte la dé finition du modèle relationnel
• R ne possède pas d'attribut composés ou multivalués

Toutes les relations que l'on a vu jusqu'à présent respectent la première forme normale.

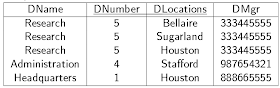
Première forme normale : exemple

     

Department

Department

Deuxième forme normale

Une relation R est en deuxième forme normale si :
   

• R est en première forme normale
• il n'y a pas d'attribut ne faisant pas partie d'une clé qui dépend d'une partie de cette clé.

Deuxième forme normale : exemple

 

Troisième forme normale

Une relation R est en troisième forme normale si :

• R est en deuxième forme normale
• il n'y a pas d'attribut ne faisant pas partie d'une clé qui dépend transitivement de cette clé

Troisième forme normale : exemple

imahe

 

Forme normale de Boyce-Codd (BCNF)

Une relation R est en BCNF si :

• R estentroisièmeformenormale
• la partie gauche de chaque DF est une clé candidate entière

La plupart des relations en troisième forme normale sont en BCNF.

Décomposition

  

Décomposition sans perte

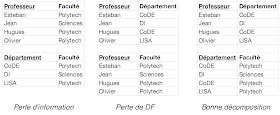
Lors de la décomposition, il faut veiller à ne perdre ni information ni dépendance fonctionnelle.

Soit une relation R décomposée en deux relations R1et R2. Si l'ensemble des attributs communs de R1et R2 est une clé d'une des deux relations, alors la décomposition est sans perte d'information.

Si dans une relation R on peut trouver trois ensembles d'attributs A,B et C tel qu'il existe une dépendance fonctionnelle A --> B, alors R peut être décomposée en deux relations R1(A; B) et R2(A; C) sans perte d'information.

-------------------------------------------------------------------------------------------------------

Exercices d'application avec Corrigés