Exercice 1
Soit R1 (A, B, C, D, E, F) une relation avec l'ensemble de dépendances suivant :
1. Donner le graphe(ensemble) minimum de dépendances. Quelles est la clé de R1 ?
2. Quelle est la forme normale de R1 ?
3. On décompose la relation R1 en R11 et R12 : R11(A, B, D, E, F) et R12(B,C). Quelles sont les formes normales des relations R11 et R12 ?
4. Proposer une décomposition sans perte d'information de R11.
Exercice 2
Soit le schéma de la relation R(A, B, C, D, E, G) et un ensemble donné de dépendances fonctionnelles pour cette relation:
1. Donner le graphe minimal des dépendances fonctionnelles de R
2. Donner une décomposition de R en relations 3NF sans perte d'informations et sans perte de dépendances.
3.Précisez l'identifiant de chaque relation obtenue.
-------------------------------------------------------------------------------------------------------
1. L'ensemble minimum de dépendances fonctionnelles de R1 est le suivant :
3. La relation R11 est en deuxième forme normale et pas en troisième normale car il subsiste une dépendance transitive. La relation R12 est en BCNF.
4. On peut décomposer R11 en R112(D, E, F) et R112(A,B,D) sans perte d'information.
Avec A --> C et A, C --> E,on constate que A, C --> E n'est pas élémentaire et que l'on peut la remplacer par A --> E sans perte de dépendance.
Avec A --> E et A, D, E --> B, G, on constate que A, D, E --> B, G n'est pas élémentaire et que l'on peut la remplacer par A, D --> B, G sans perte de dépendance.
Avec A --> B et A, D --> B,on constate que A, D --> B est redondante et que l'on peut la supprimer.
Avec A --> B, C --> B et A --> C, on constate que A --> B peut être déduite et que l'on peut donc la supprimer.
L'ensemble minimum des dépendances fonctionnelles de R est donc le suivant :
Voici une décomposition sans perte de dépendance ni d'information :
Correction
------------------------------------------------------------------------------------------------------- Corrigé Exercice 1 :
1. L'ensemble minimum de dépendances fonctionnelles de R1 est le suivant :
2. La clé de cette relation est (A,B). Cette relation est en première forme normale mais pas en deuxième forme normale car il y a un attribut qui ne fait pas partie de la clé(C) qui dépend d'une partie de la clé(B).
3. La relation R11 est en deuxième forme normale et pas en troisième normale car il subsiste une dépendance transitive. La relation R12 est en BCNF.
4. On peut décomposer R11 en R112(D, E, F) et R112(A,B,D) sans perte d'information.
Corrigé Exercice 2
Avec A --> C et A, C --> E,on constate que A, C --> E n'est pas élémentaire et que l'on peut la remplacer par A --> E sans perte de dépendance.
Avec A --> E et A, D, E --> B, G, on constate que A, D, E --> B, G n'est pas élémentaire et que l'on peut la remplacer par A, D --> B, G sans perte de dépendance.
Avec A --> B et A, D --> B,on constate que A, D --> B est redondante et que l'on peut la supprimer.
Avec A --> B, C --> B et A --> C, on constate que A --> B peut être déduite et que l'on peut donc la supprimer.
L'ensemble minimum des dépendances fonctionnelles de R est donc le suivant :
Voici une décomposition sans perte de dépendance ni d'information :



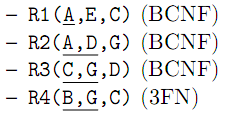
Au niveau de question 2 de l'exercice 1 qui porte sur la forme normale de R1. Le corrigé stipule que R1 est en 2FN. Or l'attribut C dépend partiellement de la clé AB à cause de la DF B->C. Cela implique que R1 n'est pas en 2FN.
RépondreSupprimerje cherche a résoudre cette exo
RépondreSupprimerLe sch ema de relation R(A;B;C;D;E;G) est-il en 2FN, 3FN ou BCNF par rapport aux
ensembles de d ependances F donn es ci-dessous ? Justi er !
(a) F = fABC ! DE;AEG ! BC;AC ! EGg
(b) F = fAB ! CE;AC ! DG;G ! A;E ! Bg
(c) F = fA ! B;B ! C;DE ! Ag
(d) F = fAC ! B;CD ! E;EG ! AD;B ! CGg