- Correction.
Corrigé Exercice 1 – Algèbre de Boole
Exercice 2 – Analyse et synthèse de circuits
1) En considérant que les portes XOR et XNOR à N entrées ont un coût 2N, calculer le coût des fonctions X, Y et Z telles qu’elles ont été implémentées.
Coût de X(A, B, C, D) = (3+1) + (2+2) = 8
Coût de Y(A, B, C, D) = (3+1) + (2+2) = 8
Coût de Z(A, B, C, D) = 8 + 8 + 2ּ2 = 20
2) Trouver l’expression disjonctive simplifiée de X au moyen de la table de Karnaugh.
Évaluer son coût minimal.
Évaluer son coût minimal.
3) Trouver l’expression conjonctive simplifiée de Y au moyen de la table de Karnaugh.
Évaluer son coût minimal.
4) Trouver l’expression conjonctive simplifiée de Z en vous basant sur les résultats précédents. Évaluer le coût minimal de cette implémentation.
5) Dessinez le circuit optimisé.
Exercice 3 – Circuits avec mux/démux
1) Trouver l’expression algébrique de X sous la forme d’un produit de sommes :
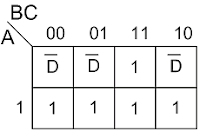
2) Donner la table de Karnaugh à variable inscrite de X sans simplifier (inscrire D) :
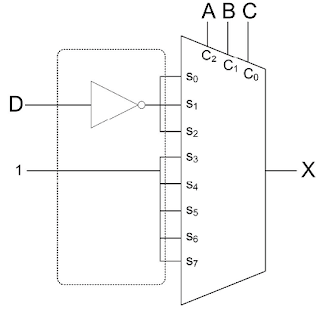
3) Dessiner dans la zone en pointillés le circuit permettant d’obtenir X en sortie
Exercice 4 - Quine-McCluskey
1) Retranscrire les maxterms de la fonction F sous forme binaire en soulignant les maxterms facultatifs :
2) Procéder par la méthode Quine-McCluskey pour simplifier la fonction F(A,B,C,D) et identifier les impliqués premiers
3) Utiliser la table suivante pour identifier les impliqués essentiels de F(A,B,C,D)
4) Les impliqués essentiels couvrent-ils l’ensemble des maxterms ? Si oui, donner l’expression conjonctive simplifiée de la fonction F(A,B,C,D). Autrement, suggérer une solution et donner l’expression conjonctive simplifiée de la fonction F(A,B,C,D) ainsi
obtenue.
L’impliqué essentiel ne suffit pas à couvrir l’ensemble des maxterms. Nous utilisons la méthode de Petrick pour terminer.
obtenue.
L’impliqué essentiel ne suffit pas à couvrir l’ensemble des maxterms. Nous utilisons la méthode de Petrick pour terminer.
5) Confirmer votre résultat en utilisant une table de Karnaugh











Je ne suis pas d'accord avec la réponse b) de l'exercice 1.
RépondreSupprimerEn effet vous dites qu'un Ou exclusif est égal à :
a./(b)./(a).b
or un Ou exclusif est égal à :
a./(b)+/(a).b
Ce qui change le résultat et le transforme en /(a)
Voila!
Si je me suis trompé veuillez m'excuser de ce mal entendu ...
Cordialement...
Merci bcp pour le cours
RépondreSupprimer