Objectifs : - Définir les opérations logiques fondamentales.
- Représenter physiquement un circuit logique.
- Utiliser la logique de boole.
Exercice 1 : Montrez la table de vérité du circuit suivant :
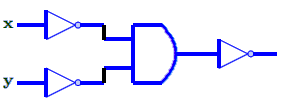
Exercice 2 : Quelle est la fonction logique réalisée par le circuit de la figure suivante :
Exercice 3 : Quelle est la fonction logique réalisée par le circuit de la figure suivante :
Exercice 4 : Utilisez l'algèbre de Boole pour simplifier les équations logiques suivantes :
Exercice 5 : Utilisez la table de Karnaugh pour simplifier l'équation logique suivante :
Exercice 6 : On dispose de 2 nombres binaires x et y à 3 bits chacun tels que x = [x2x1x0] et y = [y2y1y0]. On veut concevoir un circuit qui fait la comparaison entre ces 2 nombres de telle sorte que la sortie S soit égale à " 1 " si dans l'ordre on a : x2:x1:x0 = y2:y1:y0 et à " 0 " autrement.
Exercice 7 : On désire effectuer la somme OU logique du contenu de deux registres A et B de 4 bits chacun selon l'équation suivante :
B <= A + B
C'est-à-dire que le résultat du contenu de A OU du contenu de B sera stocké dans le registre B. Chaque bit du registre A est désigné par : Ai et chaque bit du registre B est désigné par : BiEn utilisant des bistables asynchrones R-S :
1. établir la table d'état contenant les colonnes Ai et Bi au temps t, Bi au temps t+1 et les entrées du bistable R-S.
2. l'expression logique du circuit.
3. le schéma logique du circuit.
Exercice 8 : On demande de simplifier une fonction logique s définie par sa forme canonique et sa table de vérité telle que :
Exercice 9 : On demande de simplifier une fonction logique s définie par sa forme canonique et sa table de vérité telle que :
------------------------------------------------------------------------






Merci
RépondreSupprimer