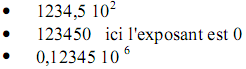Cours Représentation des nombres Cours Architecture des ordinateurs Codage des nombres
Objectifs : - Représentation des nombres entiers.
- Représentation des nombres décimaux.
- Représentation des nombres décimaux.
1) Introduction
Les systèmes informatiques travaillent sur des longueurs fixes de bits appelées MOT.
Un MOT est la plus grande série de bits qu'un ordinateur puisse traiter en une seule opération.
Exemple : la famille de microprocesseur actuelle utilise des mots de 32 bits ou plus récemment 64 bit
L'entité de base de l’information sur un système informatique est l'octet (8 bits). Néanmoins, les nombres peuvent être codés de différentes façons. Il est important de bien comprendre comment se présentent les nombres dans divers format afin de :
- Minimiser la place occupée sur le support de stockage.
- Mais aussi la place occupée en mémoire centrale et donc la rapidité des traitements que l'on fera sur ces données.
2) Les nombres entiers
La première codification des nombres consiste à les coder de façon naturelle sur les mots connus au niveau de la machine, 8 16 ou 32 bit la limitation étant la valeur maximale que l'on peut stocker. On parle alors de représentation en champs fixe.
2.1 - Les nombres naturels
Par nombre naturel, on entend les nombres entiers, positifs ou nuls.
1 octet pourra coder un nombre de 0000 00002=> 1111 11112 (0 => 255)
1 mot de 16 bits : de 0 => 216 -1 (65535)
1 mot de 32 bits : de 0 => 232 -1 (4 294 967 295)
La limite reste toujours la taille du mot manipulé.
1 octet pourra coder un nombre de 0000 00002=> 1111 11112 (0 => 255)
1 mot de 16 bits : de 0 => 216 -1 (65535)
1 mot de 32 bits : de 0 => 232 -1 (4 294 967 295)
La limite reste toujours la taille du mot manipulé.
2.2 - Les nombres relatifs
La vie n'étant pas faite que de choses positives, il a fallu introduire les nombres négatifs. Leur représentation est réalisé grâce au bit de poids fort.
On parle également d'entiers signés.
- Nombres positifs => le bit de poids fort est 0
- Nombres négatifs => le bit de poids fort est 1
Partant de ce principe, il existe différentes techniques pour représenter les nombres négatifs :
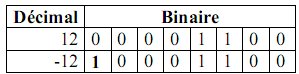
2.2.1 Représentation par signe et valeur absolue :
Le nombre négatif est codé de la manière suivante :
- Le bit de poids fort est à 1
- Les autres bits contiennent la valeur absolue du nombre
Exemple sur un octet :
Un inconvénient de cette méthode est que pour réaliser des opérations entre nombres signés, il faut faire un traitement particulier du bit de signe. Le résultat final ne pouvant être obtenu de façon simple (addition ou
soustraction des deux nombres).
Une solution a été trouvée, c'est celle de l’utilisation du complément à 2. Celui-ci s'obtient en ajoutant 1 au complément à 1.
Un inconvénient de cette méthode est que pour réaliser des opérations entre nombres signés, il faut faire un traitement particulier du bit de signe. Le résultat final ne pouvant être obtenu de façon simple (addition ou
soustraction des deux nombres).
Une solution a été trouvée, c'est celle de l’utilisation du complément à 2. Celui-ci s'obtient en ajoutant 1 au complément à 1.
2.2.2 Représentation par le complément à 1 :
Le complément à 1 (noté C1) est également appelé complément logique, il consiste à inverser chaque bit (0 => 1 et 1 => 0).
- L‘enter positif est représenté sous sa forme naturelle.
- L‘enter négatif est représenté par le complément à 1.
2.2.3 Représentation par le complément à 2 :
Le complément à 2 (noté C2) est également appelé complément vrai, il consiste à ajouter 1 en binaire au complément à 1.
- L‘enter positif est représenté en binaire naturel.
- L‘enter négatif est représenté par le complément à 2 de son opposé.
Exemple sur un octet:
A partir de ce moment, il devient aisé de réaliser des opérations sur des nombres signés, une soustraction a-b devenant une addition a + (-b). (-b) étant le complément à 2 de b
Exemple : 17-12
Le résultat se lit directement.
A partir de ce moment, il devient aisé de réaliser des opérations sur des nombres signés, une soustraction a-b devenant une addition a + (-b). (-b) étant le complément à 2 de b
Exemple : 17-12
Le résultat se lit directement.
- Si le bit de poids fort est 0, le résultat est positif
- Si le bit de poids fort est 1, le résultat est négatif
Exemple : 5-12
Ici, le résultat est négatif. Pour en connaître la valeur absolue, il suffit de faire le complément à 2 du résultat :
La valeur absolue du résultat est 0000 0001112 => 710
5 - 12 = -7 CQFD
Exercices :
2.2.4 Les limites des nombres
Les nombres sont codés de façon fixe, ce qui fait qu'ils ont une limite liée au nombre de bis qui les représentent :
En synthèse, si la puissance de 2 est n, les valeurs vont de -2" à 2" -1
3) Les nombres décimaux
3.1 - Représentation en virgule fixe
Dans cette représentation, la position de la virgule est laissée à l'appréciation du programmeur. En fait, il s'agit uniquement d'un format d'affichage.
Exemple, les prix sur une facture sont représentés systématiquement avec 2 chiffres derrière la virgule. 12,50 Euros sera représenté comme 1250.
- Dans cette représentation, les nombres décimaux sont représentés comme des entiers dans l’ordinateur.
- Le programmeur sait que les chiffres ont 2 chiffres derrière la virgule.
- Il lui appartient de placer la virgule lors de l’affichage
- De la même manière, il placera le sigle derrière le montant
3.2 - Représentation en virgule flottante
La représentation en format fixe présente l'inconvénient majeur de sa taille à savoir le nombre est limite Pour
passer cette limitation, Une représentation existe à savoir la représentation en virgule flottante. Cette représentation des nombres est basée sur la décomposition en :
- Une parte fixe représentant les chiffres : La mantisse
- Une parte variable représentant la puissance de 10 de la parte fixe : l'exposant
Une représentation en virgule flottante n‘est pas unique, on pourrait aussi écrire :
Il faut donc les représenter sous une forme normalisée afin que la représentation ne varie pas d‘un
logiciel à un autre.
3.2.1 La forme normalisée
Un nombre normalisé en virgule flottante est un nombre dans lequel le chiffre qui précède la virgule est un 0 et
le chiffre qui suit la virgule n‘est pas un 0
Ce 0 est omis dans l'écriture de la mantisse et le nombre est stocké comme un entier :
3.2.2 Le codage dans la machine
L'écriture en virgule flottante est normalisée par L'IEEE .
La forme d'écriture sur 32 bits (simple précision) prendra ce format :
Dans l’exemple ci-dessus, on codera 123456 comme mantisse => 1E240
on codera 6 comme exposant=> 6
Le nombre s'écrit alors :
Attention, cette représentation en fonction de la taille des nombres peut amener un arrondi, la mantisse n'étant
que sur 23 bits (+ 1 bit de signe).
Article plus récent Article plus ancien