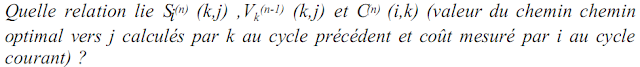Exercice Routage RIP TP Réseau Routage RIP
Routage RIP
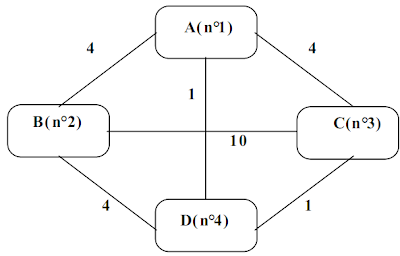
Le graphe ci -dessous représente un réseau informatique : les sommets : A, B, C, D représentent les noeuds
Plus loin dans l'exercice, on utilise des numéros pour désigner les noeuds de commutation : A est le n° 1, B est le n° 2, C est le n° 3, et D est le n° 4.
Question 1 : Calcul du routage centralisé
Pour calculer le routage optimal on utilise l'algorithme centralisé suivant (qui n'est pas le meilleur algorithme centralisé de calcul de chemin minimal dans un graphe)
Calculer à l'aide de cet algorithme le routage optimal du réseau
Déterminer, en utilisant la matrice P, l'arbre de routage (sink tree) et la table de routage du noeud A
CONSTANTES
N: entier ; % Nombre de noeuds;
Type Nom_de_noeud: entier dans (1..N); % nom des noeuds de commutation;
C : tableau (N,N) de réels ; % cout de transmission en point à point; C(i,i)=0 pour tout i
et C(i,j)=+8 si il n'y a pas de liaison entre i et j; quand
il y en a une, le coût a été porté sur l'arc du graphe ci-
dessus %;
VARIABLES
V: tableau (N,N) de réels ; % A la fin de l'algorithme V(i,j) est égal au coût du chemin
de valeur minimale de i vers j %;
P: tableau (N,N) de Nom_de_noeuds; % A la fin de l'algorithme P(i,j) est le successeur
de i dans le chemin optimal de i vers j%;
Iter: entier; % numéro d'itération%;
cout: réel;
i,j,k,r: Nom_de_noeuds;
CORPS DE PROCEDURE (Ford)
Calculer à l'aide de cet algorithme le routage optimal du réseau
Déterminer, en utilisant la matrice P, l'arbre de routage (sink tree) et la table de routage du noeud A
CONSTANTES
N: entier ; % Nombre de noeuds;
Type Nom_de_noeud: entier dans (1..N); % nom des noeuds de commutation;
C : tableau (N,N) de réels ; % cout de transmission en point à point; C(i,i)=0 pour tout i
et C(i,j)=+8 si il n'y a pas de liaison entre i et j; quand
il y en a une, le coût a été porté sur l'arc du graphe ci-
dessus %;
VARIABLES
V: tableau (N,N) de réels ; % A la fin de l'algorithme V(i,j) est égal au coût du chemin
de valeur minimale de i vers j %;
P: tableau (N,N) de Nom_de_noeuds; % A la fin de l'algorithme P(i,j) est le successeur
de i dans le chemin optimal de i vers j%;
Iter: entier; % numéro d'itération%;
cout: réel;
i,j,k,r: Nom_de_noeuds;
CORPS DE PROCEDURE (Ford)
Question 2 : Algorithme réparti adaptatif (Mac Quillan)
Dans une version d'Arpanet, le routage adaptatif était réalisé en utilisant un algorithme adaptatif réparti dérivé du précédent. Dans cet algorithme le noeud i calcule uniquement la ième ligne des matrices V et P (soit le coût de transmission d'un message de i vers tous les autres noeuds du réseau et l'adjacent préféré de i vers tous les noeuds du réseau). Pour cela, il envoie périodiquement à ses voisins V(i,•) et reçoit de chacun d'entre eux la ligne de V correspondante. L'algorithme s'adapte aux variations des coûts qui sont mesurés à chaque itération.
Algorithme Arpa(i)
cycle
Attendre T secondes;
pour tout voisin k de i
Envoyer V(i,•);
Recevoir V(k,•);
Mesurer C(i,k);
finpour
-- Les données sont prêtes pour une itération du calcul
Appliquer la partie A de l'algorithme précédent pour trouver
les nouvelles valeurs de V(i,•) et P(i,•);
Déterminer la nouvelle table de routage de i;
fincycle
La mesure avec Mesurer C(i,k) peut s’effectuer de plusieurs façons différentes. Par exemple on peut considérer que le coût d’une ligne est infini si sur un hôte, la file de messages en émission vers un destinataire est pleine, et vide en réception depuis celui-ci.
On suppose qu'à l'instant t=0 tous les noeuds ont calculé les valeurs respectives de V(i,•) et P(i,•) et la table de routage correspondante. La liaison (3,4) tombe en panne. Chaque noeud commence une étape du cycle de calcul.
Appliquer l'algorithme pour la première itération (numérotée n).
Il est recommandé de retracer le graphe à grande échelle et d'associer au noeud i la matrice Si (voir pages suivantes).
Il est recommandé de retracer le graphe à grande échelle et d'associer au noeud i la matrice Si (voir pages suivantes).
Question 3
Pendant la première itération, un paquet part d'un calculateur hôte connecté au noeud de commutation 1 pour être transmis a un hôte connecté au noeud 3.
Que se passe t'il ? Compléter les élements ci-dessous
Les valeurs de V et P sont stabilisées après plusieurs itérations si on suppose que les coûts ne sont plus modifiés durant cette phase de calcul. Les itérations n+1, n+2, n+3 sont données ci -dessous.
Cette solution est optimale, l’itération suivante donnerait le même résultat !!!
Remarque : Il est possible que certaines erreurs se soient glissées dans les calculs, mais elles ne gènent en rien la réponse à la dernière question.
Article plus récent Article plus ancien