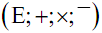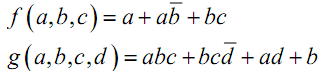Cours Algèbre de boole La logique combinatoire et Diagrammes de Karnaugh
Algèbre de BOOLE
Définition et vocabulaire
=> Analogies entre logique des propositions et ensembles
Considérons le tableau suivant :
Remarques :
- F correspond à toute proposition dont la table de Boole ne contient que des 0 ; V correspond à toute proposition dont la table de Boole ne contient que des 1.
- La deuxième équivalence est connue sous le nom de « théorème de contradiction » (une proposition et son contraire ne peuvent être vraies (ou fausses) toutes les deux !).
- La troisième équivalence est connue sous le nom de « théorème du tiers exclu » (une proposition est soit vraie soit fausse … il n’y a pas d’autre possibilité).
L’algèbre de Boole va permettre de formaliser ces analogies dans un autre langage reposant sur les équivalences suivantes :
Considérons alors un ensemble E sur lequel on a défini une addition notée « + », une multiplication notée « . » ou « × » et une application.
On dira que
est une algèbre de Boole si pour tout triplet (a;b;c) d’éléments de E on a :
ATTENTION ! « 0 » et « 1 » sont des notations facilitant la lisibilité mais ne désignant pas les réels 0 et 1 !
Remarques :
- Comme dans R , la multiplication est prioritaire sur l’addition. Le parenthésage et l’écriture des opérations en découlent.
- L’addition et la multiplication booléennes ne sont pas l’addition et la multiplication réelles.
=> Algèbre de Boole des propositions
Théorème
L’ensemble des propositions muni des connecteurs ET et OU et de l’application : P → NON P est une algèbre de Boole.
Remarques :
Les connecteurs ET et OU jouent les rôles respectifs de la multiplication et de l’addition ;
F , V et <=> sont équivalents à 0, 1 et =.
=> Algèbre de Boole et parties d’un ensemble
Théorème
Soit E un ensemble quelconque.
L’intersection et la réunion jouent les rôles respectifs de la multiplication et de l’addition ;
=> Algèbre de Boole et binaire
On considère un ensemble comportant deux éléments (il s’agit donc d’une paire) que l’on note 0 et 1 (il sont sans rapport avec les nombres 0 et 1).
On définit dans cet ensemble une addition et une multiplication comme suit :
On a alors le théorème suivant :
Théorème
L’ensemble {0;1} muni de l’addition, de la multiplication et de l’application
définies ci-dessus est une algèbre de Boole.
définies ci-dessus est une algèbre de Boole.
Propriétés des opérations
=> Propriétés principales d’une algèbre de Boole
Outre les huit propriétés fondamentales caractérisant une algèbre de Boole (elles doivent être vérifiées pour que l’on puisse parler d’une telle algèbre), on doit en mentionner onze autres.
=> Algèbre de Boole, propositions et parties d’un ensemble.
Le tableau de la page suivante fournit les équivalences fondamentales existant entre l’algèbre de Boole, la logique des propositions et la théorie des ensembles.
On a fait apparaître dans l’ordre :
- les huit propriétés servant à définir une algèbre de Boole ;
- les onze propriétés additionnelles mentionnées plus haut.
Formes canoniques d’une fonction booléenne
=> Fonction booléenne.
Exemples :
=> Mintermes et maxtermes.
Un « minterme » de n variables booléennes est un produit comportant n facteurs, chaque facteur correspondant à une variable donnée ou à son complémentaire.
Un « maxterme » de n variables booléennes est une somme comportant n termes, chaque terme correspondant à une variable donnée ou à son complémentaire.
Exemple.
Soit a, b, c et d quatre variables booléennes.
=> Formes canoniques disjonctive et conjonctive d’une fonction booléenne.
Cette somme est appelée « forme disjonctive » de f.
De façon analogue, il est possible d’écrire f sous la forme d’un produit de maxtermes.
Ce produit est appelé « forme conjonctive » de f.
Exemple.
On a :
Par ailleurs, on a :
Diagrammes de Karnaugh
Note : dans cette partie, on ne considère que des variables booléennes binaires (typiquement, ne pouvant prendre que les valeurs logique 0 ou 1).
=> Définition
Un diagramme de Karnaugh est un moyen simple de représenter une expression (ou fonction) booléenne comportant un nombre donné de variables.
Il se présente sous la forme d’un tableau (voir ci-dessous) ne comportant que des 1 (les éventuelles cases comportant des 0 sont laissées vides).
Nous fournissons ci-dessous les diagrammes de Karnaugh correspondant à l’expression booléenne
(X ne vaut 1 que si a vaut 1 et b vaut 0).
=> Cas de deux variables :
=> Cas de trois variables :
On notera la disposition particulière de la première ligne dans le cas du deuxième diagramme : l’idée est de ne changer que l’une des deux valeurs (celle de b ou celle de c) en passant d’une colonne à une autre.
=> Exemples simples
Nous fournissons ci-dessous les diagrammes de Karnaugh d’expressions simples mais fondamentales : leur maîtrise permet d’identifier, dans des diagrammes plus complexes, des configurations connues et, ainsi, de simplifier des expressions booléennes.
A chaque fois, nous fournissons deux diagrammes correspondant aux deux contextes « deux variables » et « trois variables ».
- X = a
- X = ab
- X = a + b
=> Mise en œuvre des diagrammes de Karnaugh
Démontrer une égalité
Pour prouver que deux expressions sont égales, on peut montrer que leurs diagrammes de Karnaugh sont identiques.
Simplification d’expressions
Principe général : on construit le diagramme de Karnaugh de l’expression considéré. Le diagramme obtenu permet de récrire l’expression plus simplement en utilisant la propriété précédente (deux propositions sont égales si, et seulement si, leurs diagrammes de Karnaugh sont identiques).
Considérons l’expression :
On suppose que l’on travaille dans un contexte à deux variables.
On demande, à l’aide de diagrammes de Karnaugh, de simplifier X.
On commence par déterminer le diagramme de Karnaugh correspondant à X.
Le diagramme de Karnaugh de
(Note : on reconnaît, dans ce dernier diagramme, le diagramme de Karnaugh de a. A titre d’exercice simple, on peut montrer par le calcul que l’on a :X1 = a )
En effectuant la somme : X1 + X2 , on obtient finalement le diagramme de Karnaugh de X :
On regroupe les « 1 » par groupe de deux :
On en déduit finalement :
Obtention de formes canoniques
1. forme canonique disjonctive
Nous allons travailler à partir de l’exemple suivant correspondant au diagramme de Karnaugh d’une expression X non fournie :
De façon générale, la forme canonique disjonctive d’une expression (ou d’une fonction) booléenne comporte autant de mintermes que son diagramme de Karnaugh comporte de « 1 ».
2. forme canonique conjonctive
Nous allons cette fois travailler à partir de l’exemple suivant
que nous avions déjà vu (cf l’obtention, par le calcul, de la forme canonique conjonctive de cette fonction) :
que nous avions déjà vu (cf l’obtention, par le calcul, de la forme canonique conjonctive de cette fonction) :
Un maxterme est nul si, et seulement si, chaque terme du maxterme est nul.
On va donc considérer ici les « 0 » du diagramme de Karnaugh.
Par exemple, le premier « 0 » (première ligne, première colonne) correspond à : a = 0, b = 0 et c = 0. Le maxterme correspondant s’écrit immédiatement : a+b+c.
Le deuxième « 0 » (première ligne, deuxième colonne) correspond à : a = 0, b = 0 et c =1. Le maxterme correspondant s’écrit donc :
On procédant ainsi pour tous les « 0 » du diagramme, on obtient finalement :
On retrouve la forme obtenue par le calcul.
De façon générale, la forme canonique conjonctive d’une expression (ou d’une fonction) booléenne comporte autant de maxtermes que son diagramme de Karnaugh comporte de cases vides.
Article plus récent Article plus ancien