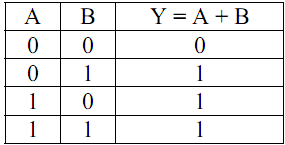Portes logiques et algèbre de Boole - Architecture des ordinateurs - tableau de karnaugh
Portes logiques et algèbre de Boole
1 Systèmes binaires
Actuellement, alors que les ordinateurs analogiques restent du domaine de la recherche, les informations traitées par les systèmes informatiques sont codées sous forme binaire. Un système binaire (signal, circuit, etc…) est un système qui ne peut exister que dans deux états autorisés. Le circuit de la figure 1 est un exemple plus que simpliste de circuit binaire : selon que l'interrupteur S est ouvert ou fermé la tension V0 ne peut être égale qu'à +5 V ou 0 V.
La réalité technique est un peu plus complexe avec des interrupteurs commandés réalisés par des transistors. Diverses notations peuvent être utilisées pour représenter ces deux états :
numérique : 1 et 0 (bit : binary digit)
logique : vrai et faux (true et false)
oui et non (yes et no)
physique : ouvert et fermé
ON et OFF
haut et bas (HI et LO, H et L, H et B)
Pour étudier les fonctions de variables binaires on utilise une algèbre développée au XIXème siècle par un mathématicien anglais : Georges Boole. Dans ce chapitre nous nous proposons de présenter les fonctions de base de l'algèbre booléenne ainsi que leurs représentations symboliques en électronique. Nous rappellerons également, sans prétendre à la rigueur mathématique, les quelques notions élémentaires nécessaires à l'étude des circuits électroniques.
L'algèbre de Boole concerne la logique des systèmes binaires. Une variable booléenne ne peut prendre que deux valeurs possibles 0 ou 1. En électronique les deux états d'une telle variable peuvent être associés à deux niveaux de tension : V(0) et V(1) pour les états 0 et 1 respectivement. On distingue les logiques positive et négative selon que V(1) > V(0) ou V(1) < V(0). Ce que nous pouvons résumer dans la table suivante donnant la signification logique des niveaux physiques :
Table 1
En pratique un niveau est défini par un domaine en tension ou en courant. Par exemple en technologie TTL, un niveau sera dit haut s'il est compris entre +2 V et +5 V et un niveau sera bas s'il est inférieur à +0.8 V. Dans la plage intermédiaire, l’état est indéterminé. Si les transitions sont inévitables, il est indispensable de traverser cette plage intermédiaire le plus rapidement possible. D’autre part, les signaux doivent être stabilisés avant d’être pris en compte par les circuits. Il y a donc des contraintes temporelles, spécifiées par les chronogrammes des feuilles de données (data sheets) fournis par les constructeurs. Dans ce cours, destiné à des informaticiens, nous n’aborderons que très peu cet aspect pratique de l’électronique.
Figure 2
Nous verrons que dans certains cas (supports magnétiques, lignes de transmission, disques optiques, etc.) l’information peut être portée par les transitions entre deux états.
2 Porte OU (inclusif)
L'opération OU (OR), encore appelée addition logique, a au moins deux entrées. La sortie d'une fonction OU est dans l'état 1 si au moins une de ses entrées est dans l'état 1. La fonction OU, notée +, est représentée par le symbole indiqué sur la figure 3 et est définie par la table de vérité suivante :
Table 2
Une table de vérité donne pour toutes les combinaisons possibles des variables logiques en entrée X, ici X = (A, B), la valeur de la fonction logique f (X).
Figure 3
Il est facile de vérifier les propriétés suivantes de la fonction OU :
(A + B) + C = A + (B + C) = A + B + C Associativité
A + B = B + A Commutativité
A + A = A Idempotence
A + 0 = A Elément neutre
A + 1 = 1 Elément absorbant
3 Porte ET
L'opération ET (AND), encore dénommée produit logique ou intersection, a au moins deux entrées. La sortie d'une fonction AND est dans l'état 1 si et seulement si toutes ses entrées sont dans l'état 1. La fonction ET, notée •, est représentée par le symbole indiqué sur la figure 4 et est définie par la table de vérité suivante :
Table 3
Figure 4
Il est facile de vérifier les propriétés suivantes de la fonction ET :
(A • B) • C = A • (B • C) = A • B • C Associativité
A • B = B • A Commutativité
A • A = A Idempotence
A • 1 = A Elément neutre
A • 0 = 0 Elément absorbant
D'autre part, les opérations ET et OU sont distributives l'une par rapport à l'autre :
A • (B + C) = (A • B) + (A • C) Distributivité du ET sur le OU
A + (B • C) = (A + B) • (A + C) Distributivité du OU sur le ET
Mentionnons également les propriétés d’absorption :
A + (A • B) = A
A • (A + B) = A
En effet :
A + (A • B) = (A • 1) + (A • B) = A • (1 + B) = A • 1 = A
A • (A + B) = (A • A) + (A • B) = A + (A • B) = A
4 Inverseur : porte NON
L'opération NON (NOT) a une seule entrée et une seule sortie. La sortie d'une fonction NON prend l'état 1 si et seulement si son entrée est dans l'état 0. La négation logique est symbolisée par un petit cercle dessiné à l'endroit où une ligne en entrée ou en sortie rejoint un symbole logique, comme par exemple sur la figure 5. La table 4 donne la table de vérité correspondante.
Table 4
Figure 5
A partir des définitions des fonctions NON, OU et ET nous pouvons déduire :
5 Théorèmes de De Morgan
De Morgan a exprimé deux théorèmes qui peuvent se résumer sous la forme suivante :
Pour vérifier le premier théorème nous remarquons que si toutes les entrées sont à 1 les deux membres de l'équation sont nuls. Par contre si une au moins des entrées est à 0 les deux membres de l'équation sont égaux à 1. Il y a donc égalité quels que soient les états des diverses entrées. Le second théorème se vérifie de la même manière : si toutes les entrées sont à 0 les deux membres de l'équation sont à 1, par contre si au moins une des entrées est à 1 les deux expressions sont à 0.
Les théorèmes de De Morgan montrent qu'une fonction ET peut être fabriquée à partir des fonctions OU et NON. De même une fonction OU peut être obtenue à partir des fonctions ET et NON. La figure 6 montre la conversion d'une porte OU en porte ET et réciproquement, utilisant le fait que :
De même, à partir des théorèmes de De Morgan nous pouvons montrer qu'une porte ET en logique positive fonctionne comme une porte OU en logique négative et vice versa.
Figure 6
6 Portes NON ET et NON OU
Une porte NON ET (NAND : NOT AND) est constituée par un inverseur à la sortie d'une porte ET (fig. 7). Une négation à la sortie d'une porte OU constitue une fonction NON OU (NOR : NOT OR) symbolisée sur la figure 8. Leurs tables de vérité respectives sont données par les tables 5 et 6 :
Comme les transistors qui interviennent comme éléments de base des portes sont par essence des inverseurs, les portes NAND et NOR sont très usitées dans la réalisation des circuits logiques. Grâce aux lois de De Morgan il est possible de réaliser des systèmes logiques avec uniquement des portes NAND ou NOR. La figure 9 montre, par exemple, comment les portes NOT, OR et AND peuvent être obtenues à partir de portes NOR.
7 Porte OU exclusif
La sortie d'une fonction OU exclusif (XOR) à deux entrées est dans l'état 1 si une entrée et seulement une est dans l'état 1. La représentation symbolique d'une fonction XOR (notée +) est donnée sur la figure 10 et sa table de vérité est la suivante :
Nous pouvons formuler de diverses manières la définition précédente :
Nous pouvons encore dire
Une fonction XOR fournit un comparateur d'inégalité :

ne vaut 1 que si A et B sont différents. Si A et B sont égaux à 1 ou si A et B sont égaux à 0 alors Y = 0. Ce qui s'écrit :
La fonction
correspond à un détecteur d'égalité. Nous avons encore la relation suivante qui peut être démontrée en utilisant les théorèmes de De Morgan :
A ces quatre relations logiques correspondent quatre circuits réalisant la fonction XOR à partir de portes OR et AND.
figure11
Mentionnons également quelques propriétés faciles à vérifier :
8 Porte à Trois Etats
La porte "3 états", ou "tri-state", n'est pas une porte logique au sens strict. Elle est principalement utilisée pour connecter une sortie sur une ligne commune à plusieurs circuits (un bus par exemple). Elle remplace généralement une porte ET. En effet, la mise en parallèle sur une même ligne de plusieurs portes ET introduit des capacités parasites. Ceci augmente les constantes de temps et a pour effet de détériorer les fronts de montée et de descente des signaux. Cela peut perturber le fonctionnement d'un système. Une porte 3 états est schématisée sur la figure suivante :
Lorsque la commande C est à 0 l'impédance de sortie est très grande : pratiquement déconnectée.
D'autre part, ces portes "3 états" fournissent une amplification de puissance.
9 Résumé des identités booléennes de base
Il est possible de montrer que toute fonction booléenne d'un nombre quelconque de variables peut s'écrire avec les trois fonctions de base ET, OU et NON. Nous avons rassemblé dans la table 9 des relations de base de l'algèbre de Boole qui nous seront utiles par la suite.
Table 9
10 Ecritures canoniques d'une fonction logique
a) Somme canonique de produits
Considérons trois variables booléennes x, y et z. A partir de ces trois variables nous pouvons construire huit produits logiques (ou minterms) Pi=0,7 faisant intervenir x ou !x, y ou !y et z ou !z. Pour chacune des huit combinaisons Ci=0,7 (000, 001, 010, etc…) des variables x, y et z, nous pouvons calculer les valeurs de ces produits. Celles-ci sont rassemblées dans la table 10.
Chacun de ces produits prend la valeur 1 pour une et une seule combinaison : Pi vaut 1 uniquement pour la combinaison Ci et 0 pour les autres combinaisons.
Considérons trois variables booléennes x, y et z. A partir de ces trois variables nous pouvons construire huit produits logiques (ou minterms) Pi=0,7 faisant intervenir x ou !x, y ou !y et z ou !z. Pour chacune des huit combinaisons Ci=0,7 (000, 001, 010, etc…) des variables x, y et z, nous pouvons calculer les valeurs de ces produits. Celles-ci sont rassemblées dans la table 10.
Chacun de ces produits prend la valeur 1 pour une et une seule combinaison : Pi vaut 1 uniquement pour la combinaison Ci et 0 pour les autres combinaisons.
Table 10
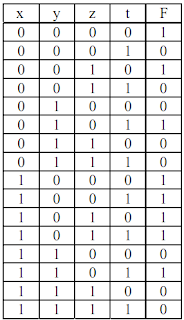
Pour toute fonction logique de trois variables x, y et z, nous pouvons écrire sa table de vérité, c'est-à-dire expliciter sa valeur pour chacune des huit combinaisons Ci. Considérons, par exemple, la fonction F dont la table de vérité est donnée dans la table 11 :
Table 11
Cette fonction F prend la valeur 1 pour la combinaison C1 comme le produit P1, la combinaison C3 comme P3 et la combinaison C4 comme P4. La fonction F prenant la valeur 0 pour toutes les autres combinaisons comme les produits P1, P3, P4, nous pouvons donc écrire que F est égale à la fonction :
F = P1 + P3 + P4
Nous pouvons vérifier cette identité dans la table 11. Nous pouvons donc exprimer F en fonction des variables x, y et z sous la forme :
Cette façon, très générale, d'écrire une fonction booléenne est appelée somme canonique de produits.
b) Produit canonique de sommes
Soient encore trois variables binaires x, y et z. Nous pouvons définir huit sommes logiques des trois variables faisant intervenir x ou !x, y ou !y et z ou !z. La table 12 donne les tables de vérité de ces sommes. Nous constatons que chacune de ces fonctions prend la valeur 0 pour une et une seule combinaison.
Table 12
Reprenons l'exemple précédent de la fonction F. Celle-ci vaut 0 pour les combinaisons C0, C2, C5, C6 et C7 en même temps que S0, S2, S5, S6 et S7. La fonction F peut donc être vue comme le produit logique de ces cinq sommes, ce qui est vérifié dans la table 13. Nous pouvons donc exprimer la fonction F sous la forme suivante :
Cette écriture est appelée produit canonique de sommes. Celle-ci est moins utilisée que la somme canonique de produits.
Table13
11 Simplification de l'écriture des fonctions logiques
a) Simplification algébrique
Simplifier une expression booléenne c'est lui trouver une forme plus condensée, faisant intervenir moins d'opérateurs et conduisant à une réalisation matérielle plus compacte. On peut simplifier une fonction par manipulation algébrique en utilisant par exemple les relations rassemblées dans la table 9. Considérons la fonction F définie par la table de vérité suivante :
Simplifier une expression booléenne c'est lui trouver une forme plus condensée, faisant intervenir moins d'opérateurs et conduisant à une réalisation matérielle plus compacte. On peut simplifier une fonction par manipulation algébrique en utilisant par exemple les relations rassemblées dans la table 9. Considérons la fonction F définie par la table de vérité suivante :
Table 14
Nous en déduisons sa forme canonique somme de produits :
Nous pouvons écrire :
Cependant cette méthode, qui demande astuce et chance, n'est pas toujours très aisée à mettre en œuvre. Nous allons maintenant décrire une méthode graphique très utile pour un nombre de variables inférieur à 6.
b) Tableaux de Karnaugh
La méthode de simplification de Karnaugh repose sur l'identité :
Elle est basée sur l'inspection visuelle de tableaux disposés de façon telle que deux cases adjacentes en ligne et en colonne ne diffèrent que par l'état d'une variable et une seule.
Si une fonction dépend de n variables il y a 2^n produits possibles. Chacun de ces produits est représenté par une case dans un tableau. Les figures suivantes donnent la structure des tableaux de Karnaugh pour 2, 3, 4 et 5 variables. Observez comment sont numérotées les lignes et les colonnes : d'une case à sa voisine une seule variable change d'état. Pour 5 variables, deux représentations sont possibles. Dans ce cas le tableau de Karnaugh peut être traité comme deux tableaux 4x4 superposés (fig. 15) ou un seul tableau de 4x8 (fig. 16).
Tableau à 2 variables
Figure 13
Figure 13
Tableau à 3 variables
Figure 14
Figure 14
Tableau à 4 variables
Figure 15
Figure 15
Tableau à 5 variables
Figure 16
Figure 16
Tableau à 5 variables
Figure 17
Figure 17
Chaque case d'un tableau correspond au seul minterm prenant la valeur 1 pour la combinaison identifiée par la ligne et la colonne. Par exemple les trois cases coloriées dans les tableaux de la figure 18 correspondent respectivement aux produits suivants :
Il faut comprendre chaque ligne et chaque colonne comme une structure cyclique continue : chaque case a toujours quatre voisins qu'il faut éventuellement chercher à l'autre extrémité de la ligne ou de la colonne. Les tableaux de la figure 18 illustrent ce concept, les croix y matérialisent les voisins des cases coloriées :
Figure 18
Dans le cas de 5 variables chaque case possède cinq voisins. Dans la représentation en tableaux superposés, quatre voisins se situent dans le même plan et le cinquième "à la verticale" dans l'autre plan. Pour la représentation plane de 8 colonnes il faut "replier" le tableau par rapport à la ligne médiane séparant les colonnes 010 et 110, qui définit un axe de symétrie. La figure 19 illustre les 5 cases voisines de la case 10101.
Figure 19
Le passage de la table de vérité au tableau de Karnaugh consiste à remplir chaque case avec la valeur de la fonction pour le produit correspondant. Il est possible de ne copier que les 1.
La méthode de simplification de Karnaugh consiste à rassembler les cases adjacentes contenant des 1 par groupes de 2, 4 ou 8 termes. Considérons en effet le groupement vertical de deux cases, en rouge, de la figure 20. Il correspond à la somme de deux termes :
Il est possible de factoriser le produit x y :
La variable t qui prend les deux valeurs 0 et 1 dans le groupement disparaît. Il ne reste que le produit des variables x et y, qui gardent ici la valeur 1.
Dans un groupement de deux termes on élimine donc la variable qui change d'état et on conserve le produit des variables qui ne changent pas. Dans un groupement de quatre on élimine les deux variables qui changent d'état. Dans un groupement de huit on élimine trois variables, etc…
On cherche à avoir le minimum de groupements, chaque groupement rassemblant le maximum de termes. Une même case peut intervenir dans plusieurs groupements car C + C = C.
C'est le cas de la case jaune sur la figure 20.
Pour les cases isolées on ne peut éliminer aucune variable. On conserve donc le produit caractérisant la case. L'expression logique finale est la réunion des groupements après élimination des variables qui changent d'état.
Reprenons l'exemple de la fonction F définie par la table de vérité 14. La figure 20 donne le tableau de Karnaugh correspondant :
Nous y observons trois groupements de deux termes, nous pouvons écrire pour la fonction :
Nous retrouvons le résultat précédent.
Considérons une autre fonction F de quatre variables x, y, z et t définie par la table 15. La figure 21 donne le tableau de Karnaugh équivalent. Sur cette figure nous avons également matérialisé les trois groupements possibles : deux groupements de quatre termes, dont un contenant les quatre coins, et un groupement de deux termes. Cette méthode nous permettent d'écrire :
12 Symboles logiques normalisés IEEE/ANSI
Nous utilisons dans ce cours les symboles logiques standards encore très fréquemment rencontrés dans l’industrie de l’électronique numérique. Cependant un ensemble de nouveaux symboles normalisés a été introduit en 1984. Il s’agit de la norme IEEE/ANSI 91-1984. Cette nouvelle norme a pour objectif de faciliter la représentation de circuits intégrés plus compliqués que les simples portes que nous utilisons ici.
Pour être le plus complet possible nous présentons ici un extrait de ces symboles normalisés :
13 Entrée trigger de Schmitt
Nous avons mentionné au début de ce chapitre que les niveaux haut et bas sont souvent caractérisés par deux seuils en tension et sont séparés par une bande indéterminée. Les fronts montants et descendants des signaux doivent alors être suffisamment rapides de manière à traverser cette zone de basculement le plus vite possible. Sinon nous pouvons observer des indéterminations avec des oscillations. C’est ce que nous observons sur le chronogramme schématisé sur la figure 24. Il représente la variation de la sortie Y (en bas) en fonction du signal d’entrée X (en haut) d’un circuit logique très simple. Nous avons schématisé des fronts lents et des parasites. Le signal de sortie ne correspond pas à ce que nous voudrions.
Pour éviter ces problèmes nous pouvons utiliser un "Trigger de Schmitt" qui déclenche sur deux seuils différents selon que le signal monte ou descend. C’est ce que nous avons schématisé sur la figure 25. La transition 0 → 1 du signal de sortie est provoquée par un signal en entrée montant et passant au-dessus du seuil haut VH. La transition 1 → 0 du signal de sortie est provoquée par un signal en entrée descendant et passant au-dessous du seuil bas VB. De cette façon nous obtenons un signal de sortie conforme à nos vœux et exempt de parasites.
Les circuits logiques pour lesquels les entrées sont filtrées par un trigger de Schmitt sont identifiés par le symbole présenté sur la figure 26. Celui-ci est ajouté à l’intérieur du symbole de la porte considérée.
Article plus récent Article plus ancien